题库组卷系统-专注K12在线组卷服务

在线咨询

当前：高中数学

当前位置：高中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

浙江省温州市苍南县金乡卫城中学2022-2023学年高一上学...

更新时间：2024-07-13 浏览次数：39 类型：月考试卷

一、单选题

1. (2022高一上·苍南月考) 已知全集 $\text{[math]}$ ，集合 $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022高一上·苍南月考) “ $\text{[math]}$ ”是“ $\text{[math]}$ ”的（）

A . 充分不必要条件 B . 必要不充分条件 C . 充要条件 D . 既不充分也不必要条件

答案解析收藏纠错 + 选题
3. (2022高一上·苍南月考) 若 $\text{[math]}$ ， $\text{[math]}$ ，则A、B的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022高一上·苍南月考) 适合条件 $\text{[math]}$ 的集合A的个数是（）

A . 15 B . 16 C . 31 D . 32

答案解析收藏纠错 + 选题
5. (2022高一上·苍南月考) 不等式 $\text{[math]}$ 的解集为（）

A . $\text{[math]}$ B . (－∞，1) C . $\text{[math]}$ ∪(1，＋∞) D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022高一上·苍南月考) 在数学漫长的发展过程中，数学家发现在数学中存在着神秘的“黑洞”现象．数学黑洞：无论怎样设值，在规定的处理法则下，最终都将得到固定的一个值，再也跳不出去，就像宇宙中的黑洞一样．目前已经发现的数字黑洞有“123黑洞”、“卡普雷卡尔黑洞”、“自恋性数字黑洞”等．定义：若一个n位正整数的所有数位上数字的n次方和等于这个数本身，则称这个数是自恋数．已知所有一位正整数的自恋数组成集合A，集合 $\text{[math]}$ ，则 $\text{[math]}$ 的子集个数为（）

A . 3 B . 4 C . 7 D . 8

答案解析收藏纠错 + 选题
7. (2022高一上·苍南月考) 对 $\text{[math]}$ ，不等式 $\text{[math]}$ 恒成立，则a的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022高一上·苍南月考) 已知实数 $\text{[math]}$ 满足 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为（）

A . 2 B . 1 C . 4 D . 5

答案解析收藏纠错 + 选题

二、多选题

9. (2022高一上·苍南月考) 已知集合 $\text{[math]}$ ，集合 $\text{[math]}$ ，下列关系正确的是（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022高一上·苍南月考) 已知 $\text{[math]}$ 且 $\text{[math]}$ ，则下列不等式正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2022高一上·苍南月考) 若“ $\text{[math]}$ ”为真命题，“ $\text{[math]}$ ”为假命题，则集合 $\text{[math]}$ 可以是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2022高一上·苍南月考) 已知关于 $\text{[math]}$ 的不等式 $\text{[math]}$ ，关于此不等式的解集有下列结论，其中正确的是（）

A . 不等式 $\text{[math]}$ 的解集可以是 $\text{[math]}$ B . 不等式 $\text{[math]}$ 的解集可以是 $\text{[math]}$ C . 不等式 $\text{[math]}$ 的解集可以是 $\text{[math]}$ D . 不等式 $\text{[math]}$ 的解集可以是 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题

13. (2022高一上·苍南月考) 命题 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. (2022高一上·苍南月考) 已知全集 $\text{[math]}$ ，集合 $\text{[math]}$ ， $\text{[math]}$ ，则下列Venn图中阴影部分的集合为．

答案解析收藏纠错 + 选题
15. (2022高一上·苍南月考) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为．

答案解析收藏纠错 + 选题
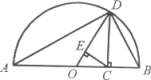
16. (2022高一上·苍南月考) 《几何原本》中的几何代数法（用几何方法研究代数问题）成了后世西方数学家处理问题的重要依据，通过这一方法，很多代数公理、定理都能够通过图形实现证明，并称之为“无字证明”.设 $\text{[math]}$ ，称 $\text{[math]}$ 为 $\text{[math]}$ 、 $\text{[math]}$ 的调和平均数.如图，C为线段AB上的点，且AC= $\text{[math]}$ ， CB= $\text{[math]}$ ，且 $\text{[math]}$ ， O为AB中点，以AB为直径作半圆.过点C作AB的垂线，交半圆于D，连结OD，AD，BD.过点C作OD的垂线，垂足为E.则图中线段OD的长度是 $\text{[math]}$ 、 $\text{[math]}$ 的算术平均数 $\text{[math]}$ ，线段CD的长度是 $\text{[math]}$ 、 $\text{[math]}$ 的几何平均数 $\text{[math]}$ ，线段的长度是 $\text{[math]}$ 、 $\text{[math]}$ 的调和平均数 $\text{[math]}$ ，该图形可以完美证明三者的大小关系为.

答案解析收藏纠错 + 选题

四、解答题

17. (2022高一上·苍南月考) 已知 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ ， $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2022高一上·苍南月考) 设集合 $\text{[math]}$ .
1. （1）若 $\text{[math]}$ ，求a的值.
2. （2）若 $\text{[math]}$ ，求实数a的取值范围.
答案解析收藏纠错 + 选题
19. (2022高一上·苍南月考) 经过长期观测得到：在交通繁忙的时段内，某公路段汽车的车流量y（千辆/小时）与汽车的平均速度 $\text{[math]}$ （千米/小时）之间的函数关系为： $\text{[math]}$ （ $\text{[math]}$ ＞0）．
1. （1）在该时段内，当汽车的平均速度 $\text{[math]}$ 为多少时，车流量最大？最大车流量为多少？（保留分数形式）
2. （2）若要求在该时段内车流量超过10千辆/小时，则汽车的平均速度应在什么范围内？
答案解析收藏纠错 + 选题
20. (2022高一上·苍南月考) 已知二次函数 $\text{[math]}$ .
1. （1）若 $\text{[math]}$ 的解集为 $\text{[math]}$ ，求不等式 $\text{[math]}$ 的解集；
2. （2）若对任意 $\text{[math]}$ ， $\text{[math]}$ 恒成立，求 $\text{[math]}$ 的最大值；
3. （3）若对任意 $\text{[math]}$ ， $\text{[math]}$ 恒成立，求 $\text{[math]}$ 的最大值.
答案解析收藏纠错 + 选题

试卷信息