江西省吉安市泰和县2021-2022学年九年级上学期期末数学...

更新时间：2022-11-14 浏览次数：31 类型：期末考试

一、单选题

1. (2021九上·泰和期末) 二次函数 $\text{[math]}$ 的顶点坐标是（　　）

A . （-2，7） B . （2，7） C . （-2，-7） D . （2，-7）

答案解析收藏纠错 + 选题
2. (2024九下·东莞模拟) 从甲、乙、丙三名男生和A、B两名女生中随机选出一名学生参加问卷调查，则选出女生的可能性是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024八下·沂源期中) 某种植基地2016年蔬菜产量为80吨，预计2018年蔬菜产量达到100吨，求蔬菜产量的年平均增长率，设蔬菜产量的年平均增长率为x，则可列方程为（）

A . 80（1+x）²=100 B . 100（1﹣x）²=80 C . 80（1+2x）=100 D . 80（1+x²）=100

答案解析收藏纠错 + 选题
4. (2022八下·长子期中) 关于反比例函数y＝ $\text{[math]}$ ，下列说法中错误的是（　　）

A . 它的图象分布在一、三象限 B . 当x＞-1时，y＜-3 C . 当x＞0时，y的值随x的增大而减小 D . 若点（a，b）在它的图象上，则（b，a）也在图象上

答案解析收藏纠错 + 选题
5. (2021九上·泰和期末) 如图，△ABC中，BD、CE是两条中线，则S_△_ADE：S_△_DEF＝（　　）

A . 2：1 B . 4：1 C . 3：1 D . 5：2

答案解析收藏纠错 + 选题
6. (2023·包头模拟) 如图，在矩形ABCD中，点E是边BC的中点，AE⊥BD，垂足为F，则tan∠BDE的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

7. (2022九上·霍邱月考) 若 $\text{[math]}$ ，则 $\text{[math]}$ 的值是．

答案解析收藏纠错 + 选题
8. (2021九上·泰和期末) 在同一时刻两根木竿在太阳光下的影子如图所示，其中木竿AB＝2m，它的影子BC＝1.5m，木竿PQ的影子有一部分落在了墙上，它的影子QN＝1.8m，MN＝0.8m，木竿PQ的长度为．

答案解析收藏纠错 + 选题
9. (2021九上·泰和期末) 如图，在菱形ABCD中，点E是CD上一点，连接AE交对角线BD于点F，连接CF，若∠AED＝50°，则∠BCF＝度．

答案解析收藏纠错 + 选题
10. (2021九上·泰和期末) 一元二次方程x²﹣4x+2=0的两根为x₁ ， x₂ ，则x₁²﹣4x₁+2x₁x₂的值为．

答案解析收藏纠错 + 选题
11. (2021九上·泰和期末) 如图，A、B两点分别在反比例函数 $\text{[math]}$ （x＞0）和 $\text{[math]}$ （x＞0）的图象上，且AB $\text{[math]}$ x轴，C为x轴上任意一点，则△ABC的面积为．

答案解析收藏纠错 + 选题
12. (2023九上·凤翔期末)
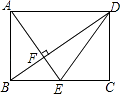
如图是一张长方形纸片ABCD，已知AB=8，AD=7，E为AB上一点，AE=5，现要剪下一张等腰三角形纸片（△AEP），使点P落在长方形ABCD的某一条边上，则等腰三角形AEP的底边长是．

答案解析收藏纠错 + 选题

三、解答题

13. (2021九上·泰和期末)
1. （1）解方程：2（x-1）＝x（x-1）；
2. （2）计算：| $\text{[math]}$ -3|+4sin45°- $\text{[math]}$ tan60°．
答案解析收藏纠错 + 选题
14. (2021九上·泰和期末) 如图，已知平行四边形ABCD，若M，N是BD上两点，且BM＝DN，AC＝2MO．
求证：四边形AMCN是矩形．

答案解析收藏纠错 + 选题
15. (2022九上·营山月考) 已知关于x的一元二次方程x²-(m-3)x-m=0
1. （1）求证：方程有两个不相等的实数根；
2. （2）如果方程的两实根为x₁、x₂ ，且x₁²+x₂²-x₁x₂=7，求m的值。
答案解析收藏纠错 + 选题
16. (2021九上·泰和期末) 如图，在所给的8×8方格纸中，每个小正方形的边长均相等，小正方形的顶点叫格点，点A，B均在格点上．请画出符合要求的格点四边形（格点四边形是指四边形的各顶点均在小正形的顶点上）．
1. （1）在图1中画出一个以AB为边的矩形．
2. （2）在图2中画出一个以AB为对角线的正方形．
答案解析收藏纠错 + 选题
17. (2021九上·泰和期末)
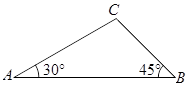
如图，在△ABC中，∠A=30°，∠B=45°，AC= $\text{[math]}$ ，求AB的长.

答案解析收藏纠错 + 选题
18. (2021九上·泰和期末) 由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图，航母由西向东航行，到达 $\text{[math]}$ 处时，测得小岛 $\text{[math]}$ 位于它的北偏东 $\text{[math]}$ 方向，且与航母相距80海里，再航行一段时间后到达B处，测得小岛 $\text{[math]}$ 位于它的北偏东 $\text{[math]}$ 方向.如果航母继续航行至小岛 $\text{[math]}$ 的正南方向的 $\text{[math]}$ 处，求还需航行的距离 $\text{[math]}$ 的长.
（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
19. (2021九上·泰和期末) 如图，在矩形ABCD中，对角线AC的垂直平分线分别与边AB和边CD的延长线交于点M，N，与边AD交于点E，垂足为点O．
1. （1）求证：△AOM≌△CON；
2. （2）若AB＝4，AD＝8，求AE的长．
答案解析收藏纠错 + 选题
20. (2021九上·泰和期末) 为助力泰和县“四城同创”（全国文明城市、全国卫生县城、国家森林城市、省级生态园林城市）工作深入开展，某校组织志愿者进行宣传活动．班主任陈老师决定从4名女班干部（小悦、小惠、小艳和小倩）中通过抽签的方式确定2名女生去参加．
抽签规则：将4名女班干部姓名分别写在4张完全相同的卡片正面，把四张卡片背面朝上，洗匀后放在桌面上，陈老师先从中随机抽取一张卡片，记下姓名，再从剩余的3张卡片中随机抽取第二张，记下姓名．
1. （1）该班男生“小刚被抽中”是　　事件，“小悦被抽中”是　　事件（填“不可能”或“必然”或“随机”）；第一次抽取卡片“小悦被抽中”的概率为　　；
2. （2）试用画树状图或列表的方法表示这次抽签所有可能的结果，并求出“小惠和小艳被同时抽中”的概率．
答案解析收藏纠错 + 选题
21. (2021九上·泰和期末) 某商场经营某种品牌的玩具，购进的单价是30元，根据市场调查，在一段时间内，销售单价是40元时，销售量是600元，而销售单价每涨1元，就会少售出10件玩具．
1. （1）设该种品牌玩具的销售单价为x元，请你分别用x的代数式来表示销售量y件和销售该品牌玩具获利利润W元；
2. （2）在（1）的条件下，若商场获利了10000元销售利润，求该玩具销售单价x应定为多少元？
3. （3）在（1）的条件下，若玩具厂规定该品牌玩具销售单价不低于45元，且商场要完成不少于480件的销售任务，求商场销售该品牌玩具获利的最大利润是多少元？
答案解析收藏纠错 + 选题
22. (2021九上·泰和期末) 如图，正方形ABCD的边长为4，E是BC边的中点，点P在射线AD上，过P作PF⊥AE于F．
1. （1）求证：△PFA∽△ABE；
2. （2）当点P在射线AD上运动时，设PA=x，是否存在实数x，使以P，F，E为顶点的三角形也与△ABE相似？若存在，请求出x的值；若不存在，说明理由．
答案解析收藏纠错 + 选题
23. (2021九上·泰和期末) 如图，抛物线 $\text{[math]}$ 的对称轴为直线x＝-1，与x轴相交于A、B两点，与y轴相交于C，OA＝OC，点A的坐标为（-3，0）．
1. （1）求抛物线的表达式；
2. （2）若点P在抛物线上，且 $\text{[math]}$ ，求点P的坐标；
3. （3）设点Q是线段AC上的动点，作QD⊥x轴交抛物线于点D，求线段QD长度的最大值．
答案解析收藏纠错 + 选题