 B .
B .  C .
C .  D .
D . 

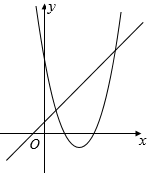 B .
B . 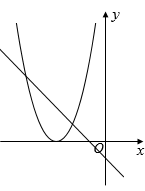 C .
C . 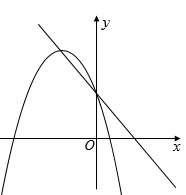 D .
D . 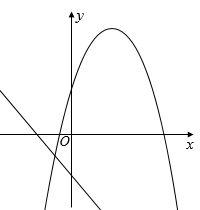
①若 ,则
;②若方程
有两个不相等的实根,则方程
必有两个不相等的实根;③若
是方程
的一个根,则一定有
成立;④若
是一元二次方程
的根,则
.
其中正确的有( )
(Ⅰ)若连续两次降价后每千克32元,且每次下降的百分率相同,求每次下降的百分率;
(Ⅱ)若按现售价销售,每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,超市决定采取适当的涨价措施,但超市规定每千克涨价不能超过8元,若每千克涨价1元,日销售量将减少20千克.现该超市希望每天盈利6000元,那么每千克应涨价多少元?
(Ⅲ)在(Ⅱ)的基础上,利用函数关系式求出每千克水果涨价多少元时,超市每天可获得最大利润?最大利润是多少?
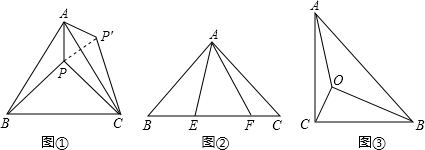
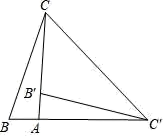
为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出∠APB=;
请你利用第(1)题的解答思想方法,解答下面问题:
已知如图②,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2;
如图③,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,求OA+OB+OC的值.