河南省洛阳市汝阳县锦程学校2022-2023学年九年级上学期...

更新时间：2024-07-13 浏览次数：44 类型：月考试卷

一、单选题

1. (2022九上·汝阳月考) 下面四个图形分别是绿色食品、节水、节能和回收标志，在这四个标志中，是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024九上·乐昌期末) 若关于x的一元二次方程 $\text{[math]}$ 没有实数根，则实数m的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023九上·仁寿月考) 在同一平面直角坐标系内，将函数y=2x²+4x﹣3的图象向右平移2个单位，再向下平移1个单位得到图象的顶点坐标是（）

A . （﹣3，﹣6） B . （1，﹣4） C . （1，﹣6） D . （﹣3，﹣4）

答案解析收藏纠错 + 选题
4. (2022九上·汝阳月考) 如图，将△ABC绕点C顺时针方向旋转40°得△A’CB’ ，若AC⊥A’B’ ，则∠BAC等于（）

A . 50° B . 60° C . 70° D . 80°

答案解析收藏纠错 + 选题
5. (2022九上·汝阳月考) 如图，PA，PB分别与⊙O相切于A，B两点，若∠C＝65°，则∠P的度数为（　　）

A . 65° B . 130° C . 50° D . 100°

答案解析收藏纠错 + 选题
6. (2022九上·汝阳月考) 如图，AB是⊙O的直径，弦CD交AB于点E，且AE=CD=8，∠BAC= $\text{[math]}$ ∠BOD，则⊙O的半径为（　　）

A . 4 $\text{[math]}$ B . 5 C . 4 D . 3

答案解析收藏纠错 + 选题
7. (2022九上·汝阳月考) 如图，⊙O的半径为1，A，B，C是圆周上的三点，∠BAC=36°，则劣弧BC的长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022九上·汝阳月考) 四张分别画有平行四边形、等腰直角三角形、正五边形、圆的卡片，它们的背面都相同，现将它们背面朝上，从中任取一张，卡片上所画图形恰好是中心对称图形的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022九上·汝阳月考) 如图2，在平面直角坐标系中，点 $\text{[math]}$ 的坐标为（1，4）、（5，4）、（1、 $\text{[math]}$ ），则 $\text{[math]}$ 外接圆的圆心坐标是

A . （2，3） B . （3，2） C . （1，3） D . （3，1）

答案解析收藏纠错 + 选题
10. (2022九上·汝阳月考) 抛物线y＝ax²＋bx＋c(a≠0)的对称轴为直线x＝－1，与x轴的一个交点在(－3，0)和(－2，0)之间，其部分图象如图，则下列结论：①4ac－b²＜0；②2a－b＝0；③a＋b＋c＜0；④点(x₁ ， y₁)，(x₂ ， y₂)在抛物线上，若x₁＜x₂ ，则y₁＜y₂.正确结论的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题

11. (2022九上·汝阳月考) 二次函数y=4（x﹣3）²+7的图象的顶点坐标是．

答案解析收藏纠错 + 选题
12. (2022九上·汝阳月考) 若点 $\text{[math]}$ 与点 $\text{[math]}$ 关于原点对称，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
13. (2022九上·汝阳月考) 用圆心角为120°，半径为9的扇形围成一个圆锥侧面，则这个圆锥的底面直径为．

答案解析收藏纠错 + 选题
14. (2022九上·汝阳月考) 从甲、乙、丙、丁4名三好学生中随机抽取2名学生担任升旗手，则抽取的2名学生是甲和乙的概率为 .

答案解析收藏纠错 + 选题
15. (2022九上·汝阳月考) 如图，在Rt△ABC中，∠BAC=30°，以直角边AB为直径作半圆交AC于点D，以AD为边作等边△ADE，延长ED交BC于点F，BC=2 $\text{[math]}$ ，则图中阴影部分的面积为．（结果不取近似值）

答案解析收藏纠错 + 选题

三、解答题

16. (2022九上·汝阳月考) 用适当的方法解下列方程．
1. （1） 3x（x+3）＝2（x+3）
2. （2） 2x²﹣4x﹣3＝0．
答案解析收藏纠错 + 选题
17. (2022九上·汝阳月考) 如图，在平面直角坐标系中，已知 ABC的三个顶点的坐标分别为A（－1，1），B（－3，1），C（－1，4）．

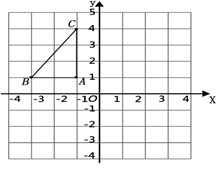
⑴画出△ABC关于y轴对称的图形；

⑵将△ABC绕着点B顺时针旋转90°后得到△A₂BC₂ ，请在图中画出△A₂BC₂ ，并求出线段BC旋转过程中所扫过的面积（结果保留）

答案解析收藏纠错 + 选题
18. (2022九上·汝阳月考) 一个不透明的布袋里装有2个白球，1个黑球和若干个红球，它们除颜色外其余都相同，从中任意摸出1个球，是白球的概率为 $\text{[math]}$ 。
1. （1）布袋里红球有多少个？
2. （2）先从布袋中摸出1个球后不放回，再摸出1个球，请用列表或画树状图等方法求出两次摸到的球都是白球的概率。
答案解析收藏纠错 + 选题
19. (2022九上·汝阳月考) 已知：AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使AB=AC，连结AC，过点D作DE⊥AC，垂足为E．
1. （1）求证：DC=BD；
2. （2）求证：DE为⊙O的切线．
答案解析收藏纠错 + 选题
20. (2022九上·汝阳月考) 如图，已知⊙A的半径为4，EC是圆的直径，点B是⊙A的切线CB上的一个动点，连接AB交⊙A于点D，弦EF平行于AB，连接DF，AF.
1. （1）求证：△ABC≌△ABF；
2. （2）当∠CAB=时，四边形ADFE为菱形；
3. （3）当AB=时，四边形ACBF为正方形.
答案解析收藏纠错 + 选题
21. (2022九上·汝阳月考) 温州某企业安排65名工人生产甲、乙两种产品，每人每天生产2件甲或1件乙，甲产品每件可获利15元.根据市场需求和生产经验，乙产品每天产量不少于5件，当每天生产5件时，每件可获利120元，每增加1件，当天平均每件获利减少2元.设每天安排x人生产乙产品.
1. （1）根据信息填表
  产品种类
  每天工人数（人）
  每天产量（件）
  每件产品可获利润（元）
  甲
  15
  乙
  x
  x
2. （2）若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元，求每件乙产品可获得的利润.
3. （3）该企业在不增加工人的情况下，增加生产丙产品，要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙（每人每天只能生产一件产品），丙产品每件可获利30元，求每天生产三种产品可获得的总利润W（元）的最大值及相应的x值.
答案解析收藏纠错 + 选题
22. (2022九上·汝阳月考) 如图
1. （1）问题：如图①，在Rt△ABC中，AB＝AC，D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转90°得到AE，连接EC，则线段BC，DC，EC之间满足的等量关系式为；
2. （2）探索：如图②，在Rt△ABC与Rt△ADE中，AB＝AC，AD＝AE，将△ADE绕点A旋转，使点D落在BC边上，试探索线段AD，BD，CD之间满足的等量关系，并证明你的结论；
3. （3）应用：如图③，在四边形ABCD中，∠ABC＝∠ACB＝∠ADC＝45°.若BD＝9，CD＝3，求AD的长.
答案解析收藏纠错 + 选题
23. (2022九上·汝阳月考)
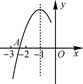
如图，二次函数y=x²+bx+c的图象交x轴于A（﹣1，0）、B（3，0）两点，交y轴于点C，连接BC，动点P以每秒1个单位长度的速度从A向B运动，动点Q以每秒 $\text{[math]}$ 个单位长度的速度从B向C运动，P、Q同时出发，连接PQ，当点Q到达C点时，P、Q同时停止运动，设运动时间为t秒．
1. （1）求二次函数的解析式；
2. （2）如图1，当△BPQ为直角三角形时，求t的值；
3. （3）如图2，当t＜2时，延长QP交y轴于点M，在抛物线上是否存在一点N，使得PQ的中点恰为MN的中点？若存在，求出点N的坐标与t的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题