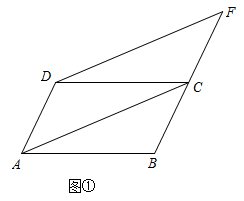
| 代表团 | 挪威 | 德国 | 中国 | 美国 | 瑞典 | 荷兰 | 奥地利 |
| 金牌数 | 16 | 12 | 9 | 8 | 8 | 8 | 7 |
应聘者 | 测试项目成绩(分) | ||
专业知识 | 语言表达 | 社会实践 | |
80 | 70 | 90 | |
90 | 55 | 80 | |
80 | 75 | 70 | |
80 | 85 | 80 | |
学生立定跳远测试成绩的频数分布表
分组 | 成绩 | 频数 |
第一组 | ||
第二组 | 12 | |
第三组 | ||
第四组 | 10 |
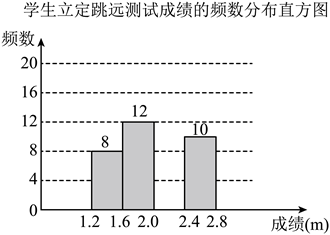
请根据图表中所提供的信息,完成下列问题:

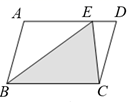
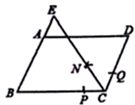
平行四边形的判定定理2 一组对边平行且相等的四边形是平行四边形.
我们可以用演绎推理证明这一结论.
已知:如图,在四边形中,AB
CD且
.
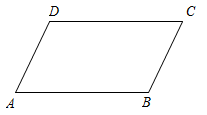
求证:四边形是平行四边形.
证明:连接 .