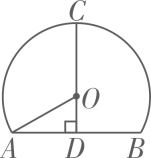一、选择题(每小题只有一个选项符合题意,请将所选选项填涂在答题卡上.本大题共10个小题,每小题3分,共30分)
-
-
A . ax2+bx+c=0
B . 2x2-1=3x
C . x2+ -3=0
D . 2x2-y=1
-3=0
D . 2x2-y=1
-
A . (1;1)
B . (1,-1)
C . (-1,1)
D . (-1,-1)
-
A . 概率很小的事情都不可能发生
B . 投掷-枚质地均匀的硬币10 000次,正面朝上的次数一定是5000次
C . 从1,2,3,4,5中任取一个数是偶数的可能性比较大
D . 13 名同学中,至少有两人的出生月份相同是必然事件
-
A . 有两个不相等的实数根
B . 有两个相等的实数根
C . 没有实数根
D . 无法确定;
-
6.
(2022·岳池模拟)
如图,在⊙O中,点C在

上.若

=

, ∠AOB=120°,则∠BCD的度数为( )

A . 60°
B . 30°
C . 150°
D . 90°
-
7.
(2022·岳池模拟)
将抛物线y=3x
2-2先向右平移3个单位长度,再向下平移2个单位长度得到新抛物线的函数解析式为( )
A . y=3(x+3)2-4
B . y=3(x-3)2
C . y=3(x-3)2-4
D . y=3(x+3)2
-
8.
(2022·岳池模拟)
“抖音直播带货”已经成为一种热门的销售方式,某抖音主播代销某一品牌的电子产品(这里代销指厂家先免费提供货源,待货物销售后再进行结算,未售出的由厂家负贵处理).销售中发现当每件产品的售价为99元时,日销售量为200件,当每件产品每下降5元时,日销售量会增加10件.已知每售出1件产品,该主播需支付厂家和其他费用共50元,设每件产品的售价为x元,主播每天的利润为w元,则w与x之间的函数解析式为( )
A . w=(99-x)[200+10(x-50)]
B . w=(x-50)[200+10(99-x)]
C . w=(x-50)(200+ ×10)
D . w=(x-50)(200+
×10)
D . w=(x-50)(200+ ×10)
×10)
-
9.
(2022·岳池模拟)
如图是某高速公路的一个隧道的横截面,若它的形状是以点O为圆心,线段OA的长为半径的圆的一部分,路面AB=12米,隧道高CD=9米,则⊙O的半径OA= ( )
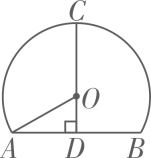
A . 6米
B .  米
C . 7米
D .
米
C . 7米
D .  米
米
-
10.
(2022·岳池模拟)
如图是抛物线y=ax
2+bx+c(a≠0)的一部分,其对称轴为直线x=2,且抛物线与x轴的一个交点坐标为(-2,0),下列结论:①b>0;②方程ax
2+bx+c=0的两个根是x
1=-2,x
2=6;③12a+c>0;④当y>0时,x的取值范围是-2<x<2;⑤若m为任意实数,则am
2+bm-12a≤-16a.其中结论正确的有( )

A . 1个
B . 2个
C . 3个
D . 4个
二、填空题(请把最简答案填写在答题卡相应的位置.本大题共6个小题,每小题3分,共18分)
-
-
-
13.
(2022·岳池模拟)
在一个不透明的布袋中,有红球、黑球、白球共60个,它们除颜色外其他都相同.小明从中任意摸出一个球,查看颜色后放回并摇匀,通过多次摸球试验后,发现摸到红球、黑球的频率分别稳定在0.15和0.45,则他估计布袋中白球的个数约是
个.
-
14.
(2022·岳池模拟)
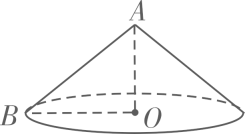
某盏路灯照射的空间可以看成如图所示的圆锥,它的母线AB=5米,半径OB=4米,则圆锥的侧面积是
平方米(结果保留π).
-
15.
(2022·岳池模拟)
若点P(-1-2a,2a-4)关于原点对称的点在第一象限内,则a的所有整数解之和是
-
16.
(2022·岳池模拟)
如图,已知AB是⊙O的弦,AB=8,C是⊙O上的一个动点,且∠ACB=45°.若M,N分别是AB,BC的中点,则线段MN长度的最大值是

三、解答题(本大题共4个小题,第17小题5分;第18、19、20小题各6分,共23分)
-
-
18.
(2022·岳池模拟)
如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别为A(-1,5),B(-4,3),C(-2,2).

( 1 )画出与△ABC关于原点O对称的 △A1B1C1 ;
( 2 )画出将△ABC绕原点O顺时针旋转90°后得到的△A2B2C2 .
-
19.
(2022·岳池模拟)
如图,AB是⊙O的直径,点C在⊙O上,延长BC至点D,使CD=BC,连接DA并延长,与⊙O的另一个交点为E,连接AC,CE.若∠E=26°,求∠D的度数.

-
20.
(2022·岳池模拟)
已知在平面直角坐标系中,二次函数y=(1-m)x
2+2x-7(m为常数,且m≠1)与x轴有唯一的交点,一次函数y=kx+7(k为常数,k≠0)的图象经过该二次函数图象的顶点,求m,k的值.
四、实践应用题(本大题共4个小题,第21小题6分,第22、23、24小题各8分,共30分)
-
21.
(2022·岳池模拟)
[阅读材料]
已知x2+y2+8x-6y+25=0,求x,y的值. .
解:将25拆分为16和9,可得(x2+8x+16)+(y2-6y+9)=0,
即(x+4)2+(y-3)2=0,
∴.x+4=0,y-3=0,
∴x=-4,y=3.
-
(1)
[解决问题]
已知m2+n2-12n+10m+61=0,求(m+n)2023的值;
-
(2)
[拓展应用]已知a,b,c是△ABC的三边长,且b,c满足b2+c2=8b+4c-20,a是△ABC中最长的边,求a的取值范围.
-
22.
(2022·岳池模拟)
初三某班举办了一场摸牌游戏,由甲、乙两名同学进行.现有5张背面完全相同的牌,正面分别标有数字-1,2,3,5,6,将五张牌背面朝上,洗匀后放在桌子上,甲从中随机抽取一张牌后放回,乙再随机抽取一张牌.
-
(1)
请用列表或画树状图的方法,求两人抽取的数字相同的概率.
-
(2)
若两人抽取的数字差的绝对值等于1,则甲获胜;若抽取的数字差的绝对值小于1,则乙获胜,这个游戏公平吗?请用概率的知识加以解释.
-
23.
(2022·岳池模拟)
如图1,要利用一面墙(墙长为15m)建羊圈,用30m的围栏围成两个大小相同的矩形羊圈.设羊圈的一边AB长为xm,羊圈的总面积为ym
2 .

-
(1)
能否围成总面积为81m2的羊圈?若能,请求出AB的长;若不能,请说明理由.
-
(2)
如果两个矩形羊圈各开一个宽1m的门(如图2) ,在不浪费围栏的情况下,求y与x的函数解析式并写出x的取值范围,并求羊圈总面积的最大值.
-
24.
(2022·岳池模拟)
如图,已知E是正方形ABCD的边AB上的一点,延长BC到点F使AE=CF,连接DE,DF.

-
(1)
能通过旋转△DAE得到△DCP吗?说明理由.
-
(2)
连接EF,过点D作DM垂直EF于点M,交BC于点N.若BN=2,CN=3,求AE的长.
五、推理论证题(9分)
-
25.
(2022·岳池模拟)
如图,AB为⊙O的直径,CD是⊙O的弦,点E在AB的延长线上,连接OC,AD,CD∥AB,CO∥DE,∠A=22.5°.

-
-
(2)
当CD=2

时,求图中阴影部分的面积.
六、拓展探究题( 10分)
-
26.
(2022·岳池模拟)
如图,已知抛物线过点O(0,0),A(5,5), 且它的对称轴为直线x=2,B是该抛物线的对称轴上的一点,且点B在第一象限内.

-
-
-
(3)
在(2)的条件下,P是抛物线上的一个动点,当PA-PB的值最大时,求点P的坐标及PA-PB的最大值.
 B .
B .  C .
C .  D .
D .