浙江省衢州市衢江区2023年中考一模数学试题

更新时间：2023-05-27 浏览次数：162 类型：中考模拟

一、选择题(本题共有10小题，每小题3分，共30分)

1. (2023·衢江模拟) 2的相反数是（）

A . 2 B . $\text{[math]}$ C . -2 D . - $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023八上·鄞州期末) 下列图形中，属于轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023·衢江模拟) 中国科学院高能物理研究所发布，基于中国“慧眼”卫星和“极目”空间望远镜对产生于距离地球240000000 光年宇宙深处伽马射线暴的高精度测量，发现其具有迄今观测到的最大亮度，其中200000000用科学记数法表示为（）

A . 24x10⁸ B . 2.4x10⁸ C . 0.24x10¹⁰ D . 2.4x10⁹

答案解析收藏纠错 + 选题
4. (2023·衢江模拟) 下列运算正确的是（）

A . a².a³=a⁵ B . (a²)³=a⁵ C . (a+b)²=a²+b² D . (ab)²=ab²

答案解析收藏纠错 + 选题
5. (2023·衢江模拟) 不等式x≥- 2的解在数轴.上表示正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. 用配方法解方程x² +4x+1=0时，配方结果正确的是（）

A . (x-2)²=5 B . (x-2)²=3 C . (x+2)²=5 D . (x+2)²=3

答案解析收藏纠错 + 选题
7. (2023·衢江模拟) 如图，⊙0的直径CD垂直弦AB于点E，且OE =2cm， DE=7cm，则AB的长为（）

A . 4cm B . 8cm C . $\text{[math]}$ cm D . 2 $\text{[math]}$ cm

答案解析收藏纠错 + 选题
8. (2023·衢江模拟) 《九章算术方程》中讲到：“今有上和七秉，损实一斗，益之下禾二秉，而实一十斗。下禾八秉，益实一斗与上禾二秉，而实一十斗。问上、下禾实一秉各几何? ”其译文为：“今有上禾7束，减去其中果实一斗，加下禾2束，则得果实10斗；下禾8束，加果实1斗和上禾2束，则得果实10斗，问上禾、下禾1束得果实多少?设上禾、下禾1束各得果.实x，y斗，则可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023·衢江模拟) 如图，在矩形ABCD中， AB<BC，连接AC，分别以点A，C为圆心，大于 $\text{[math]}$ AC的长为半径画弧，两弧交于点M，N，直线MN分别交AD，BC于点E，F.下列结论中错误的是（）

A . 四边形AECF是菱形 B . ∠AFB= 2∠ACB C . AC.EF=CF.CD D . 若AF平分∠BAC，则CF=2BF

答案解析收藏纠错 + 选题
10. (2023九上·衢江月考) 已知二次函数y=-(x-a)²+1，当-1≤x≤3时， y的最大值为-8，则a的值为（）

A . -4或6 B . 0或6 C . -4或2 D . 2或6

答案解析收藏纠错 + 选题

二、填空题(本题共有6小题，每小题4分，共24分)

11. (2023·衢江模拟) 去括号： -(x-1)=.

答案解析收藏纠错 + 选题
12. (2023九下·衢江模拟) 已知现有的12瓶饮料中有2瓶已过了保质期，从这12瓶饮料中任取1瓶，恰好取到已过了保质期的饮料的概率是.

答案解析收藏纠错 + 选题
13. (2023·衢江模拟) 如图，在矩形ABCD中，E是BC上一点，且AE⊥BD，若AB=3， AD=4，则BE的长为.

答案解析收藏纠错 + 选题
14. (2023·衢江模拟) 如图，有一张长方形桌子的桌面长130cm，宽60cm.有-块长方形台布的面积是桌面面积的2倍，并且铺在桌面上时，各边垂下的长度相等.若设台布垂下的长度为xcm，则可列出x满足的方程为.(不必化简)

答案解析收藏纠错 + 选题
15. (2023·衢江模拟) 在平面直角坐标系中，反比例函数y= $\text{[math]}$ (k>0)的图象如图所示，等边三角形ABC的顶点A在该反比例函数图象上，AB⊥x轴于点B，OB=1.若顶点C恰好落在y= $\text{[math]}$ (k>0)的图象上，则k=.

答案解析收藏纠错 + 选题
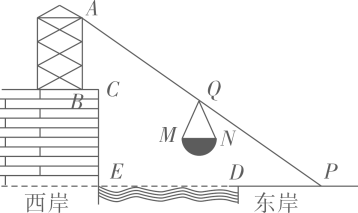
16. (2023·衢江模拟) 如图，ED为一条宽为4米的河，河的西岸建有-道防洪堤，防洪堤与东岸的高度差为
3米(即CE=3米)，因为施工需要，现准备将东岸的泥沙通过滑轨送到西岸的防洪堤上，防洪堤上已经建好一座固定滑轨一端的钢架，现准备在东岸找一个点P作为另一端的固定点，已知吊篮的截面为直径为1米的半圆(直径MN=1米)，绳子QM=QN=1.3米，钢架高度2.2米(AB=2.2米)，距离防洪堤边缘为0.5米(BC=0.5米).
1. （1）西岸边缘点C与东岸边缘点D之间的距离为米.
2. （2）滑轨在运送货物时保持笔直，要想做到运输过程中吊篮一定不会碰到点C，则DP的长度应大于米.
答案解析收藏纠错 + 选题

三、解答题(本题共有8小题，第17~19小题每小题6分，第20~21小题每小题8分，第22~23小题每小题10分，第24小题12分，共66分，请务必写出解答过程)

17. (2023·衢江模拟) 计算：
1. （1）计算：（-1）²+ $\text{[math]}$ ；
2. （2）化简： $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2023·衢江模拟) 在△ABC和△DEF中，B， E， C， F在同一条直线上，已知AB=DE， BE=CF，∠ABC=∠DEF，求证： AC=DF.

答案解析收藏纠错 + 选题
19. (2023·衢江模拟) 我们把端点都在格点上的线段叫做格点线段.如图在6x6的方格中，现有一格点线段AB，按要求画图.
1. （1）在图1中画一个格点△ABC，使得△ABC内部有1个格点(不包括边上的格点) ；
2. （2）已知格点D，在图2中画一条格点线段DE，使线段DE和线段AB互相平分.
答案解析收藏纠错 + 选题
20. (2023·衢江模拟) 新年伊始，中国电影行业迎来了开门红，以下是春节七天《满江红》《流浪地球2》两部影片上映后全国单日票房信息.

根据以上信息，回答下列问题：
1. （1）《满江红》这七天单日票房的中位数为.
2. （2）求《流浪地球2》这七天单日票房的平均数；
3. （3）请结合统计图，从单日票房的“平均数”和“中位数”角度分析哪部电影在这七天中更受观众喜爱.
答案解析收藏纠错 + 选题
21. (2023·衢江模拟) 如图，在等腰△ABC中，AB=AC，以AC为直径作⊙0交BC于点D，过点D作⊙0的切线交AB于点E.
1. （1）求证： DE⊥AB.
2. （2）若DE= $\text{[math]}$ ， ∠C=30°，求阴影部分面积.
答案解析收藏纠错 + 选题
22. (2023·衢江模拟) “冰墩墩"和“雪容融"作为第24届北京冬奥会和残奥会的吉祥物深受大家喜爱，下图是某文旅店订购情况：
1. （1）表示出“雪容融”的单价.
2. （2）若“冰墩墩”的订购单价比“雪容融"的订购单价多20元.
  ①分别求出这两种吉祥物的数量.
  ②该文旅店分别以100元和80元的单价销售“冰墩墩和“雪容融”，在“冰墩墩"售出一半，“雪容融”售完时，文旅店为了尽快卖完，决定对剩余的“冰墩墩”每个降价a元销售，很快全部售完，若要保证文旅店总利润不低于6200元，求a的最大值.
答案解析收藏纠错 + 选题
23. (2023·衢江模拟) 如图1，一钢球从斜面顶端A静止滚下，斜面与水平面的夹角∠ABD为30°，斜面顶端到水平线的距离AD为4dm.钢球在斜面上滚动的路程S₁是滚动时间t的二次函数，部分对应值如下表，钢球在斜面上滚动的速度v(dm/s)是时间t (s) 的正比例函数，函数图象如图2所示.
1. （1）求S₁关于t的函数表达式.
2. （2）求斜面的长度AB，以及钢球滑至底端B的速度.
3. （3）钢球滚动至有阻力的水平面BC上时，滚动路程S(dm)与时间T (s)的关系式为S =-4T²+ v₀T，v₀(dm/s)指的是钢球在点B的速度，T指的是从B开始滚动的时间。求钢球在水平面上滚动的最远距离。
答案解析收藏纠错 + 选题
24. (2023·衢江模拟) 如图，已知菱形ABCD， E为对角线AC上一点.
1. （1） [建立模型]
  如图1，连结BE， DE.求证：∠EBC=∠EDC.
2. （2） [模型应用]
  如图2， F是DE延长线上一点，∠EBF=∠ABC， EF交AB于点G.
  ①判断△FBG的形状，并说明理由.
  
  ②若G为AB的中点，且AB=4，∠ABC=60°，求AF的长.
3. （3） [模型迁移]
  F是DE延长线上一点，∠EBF=∠ABC， EF交射线AB于点G，且sin∠BAC= $\text{[math]}$ ， BF//AC.求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题