试剂盒数量n（盒） | … | 3 | 4 | 5 | 6 | 7 | 8 | … |
总价w（元） | … | 45 | 60 | 75 | 90 | 105 | 120 | … |
请从下列A，B两题中任选一题作答．我选择
A．根据图象，公路AB段的长为米．
B．根据图象，点A到公路BC的距离为米．
化简（2x-1）（2x＋1）＋（2x-3）（3-2x） 解：原式＝（2x）2-1-（2x-3）2 ……第一步 =4x2-1-（4x2-12x+9）……第二步 =4x2-1-4x2-12x-9……第三步 =-12x-10……第四步 |
①上解题过程中，第一步用到的乘法公式用字母表示为；第二步用到的乘法公式用字母表示为；
②第开始出现错误，出现错误的原因是.
AC的长x（cm） | … | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
两正方形的面积和S（cm2） | … | 12.5 | 10 | 8 | 8.5 | 12.5 | … |
变化规律为：
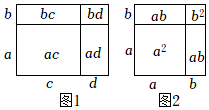
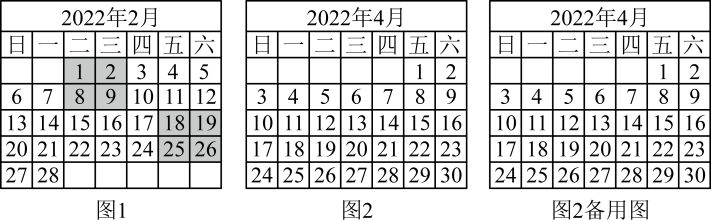
如图1是2022年2月份的日历，小宇在其中画出两个2×2的方框，每个框均框住位置为
的四个数，计算“bc-ad”的值，探索其运算结果的规律．
解：bc-ad的值均为 ▲ ． 理由如下：
设a＝x，则b＝x＋7，c＝x＋1，d＝ ▲
因为bc-ad＝ ▲
所以bc-ad的值均为 ▲
请从下列A，B两题中任选一题作答．我选择 ▲
A，在日历中用“十字框”框住位置为
的五个数，探究bc-ad的值的规律，请写出你的结论，并说明理由．
B．在日历中用日数柜框住位置为
的七个数，探究bc-ad的值的规律，请写出你的结论，并说明理由．
问题情境：
数学课上，老师让同学们以“三角板与平行线”为主题开展数学活动．如图1，已知l1∥l2 ， 直角三角板ABC中，∠B＝90°，将其顶点A放在直线l2上，并使边AB⊥直线l1于点D，AC与l1相交于点H．老师提出问题：试判断边BC与直线l1的位置关系并说明理由．
下面是小亮不完整的解答过程和解题反思，请你补充完整：
解：∠1＋∠2＝90°．过点B作直线BN∥l1 ， 如图：
∵l1∥l2（已知）
∴BN∥l2（ ）
∴∠1= ▲ ∠2= ▲ （ ）
∵∠ ▲ +∠ ▲ =∠ABC，∠ABC=90°
∴∠1＋∠2＝90°
解题反思：在图中“过点B作直线BN∥l1”的作用是 ▲
请从下列A，B两题中任选一题作答．我选择 ▲
A．在图2中作线段PO和QO，使它们分别平分∠1和∠2的对顶角，如图3．直接写出∠POQ的度数．
B．在图2中∠ABC内部作射线BE，过点B作射线BF⊥BE交直线L2于点M，得到∠3，如图4．直接写出∠1，∠3与∠EBC的数量关系．
