 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
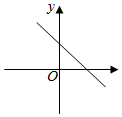 B .
B . 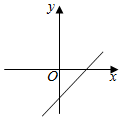 C .
C . 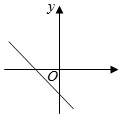 D .
D . 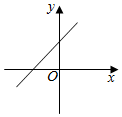

670,870,730,1140,700,690,1170,970,1000,970
730,840,1060,870,720,870,1060,930,840,870
整理数据:按如下分段整理样本数据并补至表格(表1)
用电量x(度) | ||||
人数 | a | 6 | b | 4 |
分析数据:补全下列表格中的统计量(表2)
平均数 | 中位数 | 众数 |
885 | c | d |
得出结论:
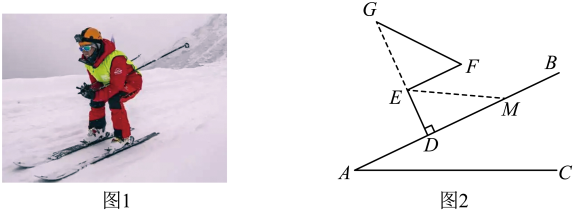
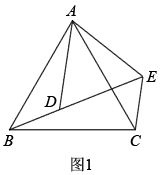
如图2所示,和
均为等腰直角三角形,
,
,
, B、D、E三点共线,线段
、
交于点F.此时,线段
、
之间的数量关系是什么?请写出证明过程并求出
的度数;
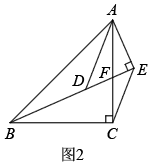
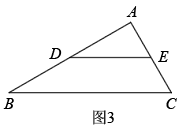
如图3所示,在中,
,
,
,
为
的中位线,将
绕点A顺时针方向旋转,当
所在直线经过点B时,请直接写出
的长.