四川省广安市岳池县2022-2023学年七年级下学期数学期中...

更新时间：2024-07-13 浏览次数：61 类型：期中考试

一、选择题(本大题共10个小题，每小题3分，共30分)

1. (2023七下·岳池期中) 在实数 $\text{[math]}$ 、 $\text{[math]}$ 、0、3.1415、 $\text{[math]}$ 、3π、3.1010010001……(相邻两个1之间的0依次增加1个)中，无理数的个数为（）

A . 3个 B . 4个 C . 5个 D . 6个

答案解析收藏纠错 + 选题
2. (2023七下·岳池期中) 2022年2月4日，第二十四届冬季奥林匹克运动会在北京隆重开幕．此次冬奥会的吉祥物“冰墩墩"是熊猫形象与冰晶外壳相结合，体现了追求卓越、引领时代以及面向未来的无限可能．在下面的四个冰墩墩图片中，能由左图经过平移得到的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023七下·岳池期中) 2022年6月5日神舟十四号载人飞船在甘肃酒泉发射升空，航天员乘组在轨工作生活6个月后于2022年12月4日返回地球，下列描述能确定飞船着陆位置的是（）

A . 内蒙古中部 B . 酒泉卫星发射中心东北方向800km处 C . 东经130°25'~98°10' D . 北纬54°35'~38°20'

答案解析收藏纠错 + 选题
4. (2023七下·岳池期中) 下列各式中，正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ =±3 C . $\text{[math]}$ =-4 D . ± $\text{[math]}$ =±11

答案解析收藏纠错 + 选题
5. (2023七下·岳池期中) 在平面直角坐标系中，有C(1，2)、D(1，-1)两点，则点D可看作是由点C （）

A . 向上平移3个单位长度得到 B . 向下平移3个单位长度得到 C . 向左平移1个单位长度得到 D . 向右平移1个单位长度得到

答案解析收藏纠错 + 选题
6. (2023七下·岳池期中) 下列命题是真命题的是（）

A . (4，3)和(3，4)表示同一个点 B . 无论x为任何实数，点(x²+1，-4)一定在第四象限 C . 垂直于同一条直线的两条直线平行 D . 相等的角是对顶角

答案解析收藏纠错 + 选题
7. (2023七下·岳池期中) 如图，给出下列条件：①∠CAD=∠ACB；②∠CAB=∠ACD；③AD∥BE且∠D=∠B；其中能推出AB∥DC的条件个数是（）

A . 0个 B . 1个 C . 2个 D . 3个

答案解析收藏纠错 + 选题
8. (2023七下·岳池期中) 将点P(m+2，3)向右平移3个单位长度到P'，且P'在y轴上，则m的值是（）

A . -5 B . 1 C . -1 D . -3

答案解析收藏纠错 + 选题
9. (2023七下·岳池期中) 如图，已知AB⊥BC，垂足为B，AB=3，点P是射线BC上的动点，则线段AP长不可能是（）

A . 5 B . 4 C . 3 D . 2.5

答案解析收藏纠错 + 选题
10. (2023七下·岳池期中) 如图，已知，∠BAC=∠ACD=90°，∠ABC=∠ADC，CE⊥AD．有下列结论：①AD∥BC；②∠ECD=∠DAC；③∠CEF=∠CFE；④CACE=∠ABC．其中正确的结论有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题(本大题共6个小题，每小题3分，共18分)

11. (2024八下·黄陂月考) 25的平方根是 .

答案解析收藏纠错 + 选题
12. (2023七下·岳池期中) 围棋起源于中国，它蕴含着中华文化的丰富内涵，是中国文化与文明的体现．如图，围棋盘放在某个平面直角坐标系内，黑棋①的坐标为(-1，-2)，白棋④的坐标为(-4，-3)，则白棋②的坐标为

答案解析收藏纠错 + 选题
13. (2024七下·滑县期中) 已知点M在第三象限，并且它到x轴的距离为1，到y轴的距离为2，则点M的坐标为

答案解析收藏纠错 + 选题
14. (2023七下·岳池期中) 若 $\text{[math]}$ +|n+3|=0，则(m+n)²⁰²³=．

答案解析收藏纠错 + 选题
15. (2023七下·岳池期中) 如图，已知三角形ABC中，∠ABC=90°，边BC=12，把三角形ABC沿射线AB方向平移至三角形DEF后，平移距离为6，GC=4，则图中阴影部分的面积为

答案解析收藏纠错 + 选题
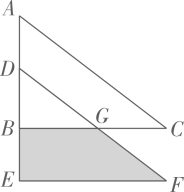
16. (2023七下·岳池期中) 在平面直角坐标系中，一个智能机器人接到的指令是：从原点O出发，按“向上→向右→向下→向右→向下→向右→向上→向右”的方向依次不断运动，每次移动1个单位长度，其移动路线如图所示，第一次移动到点 A₁ ，第二次移动到点A₂……第n次移动到点A_n ，则点A₂₀₂₃的坐标是

答案解析收藏纠错 + 选题

三、解答题(本大题共4个小题，每小题6分，共24分)

17. (2023七下·岳池期中) 计算 $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2023七下·岳池期中) 已知2(x-3)²-98=0，求x的值．

答案解析收藏纠错 + 选题
19. (2023七下·岳池期中) 如图，在正方形网格中建立平面直角坐标系，三角形ABC的三个顶点的顶点都在网格点上，已知点A(3，2)，B(4，-3)，C(1，-2)．
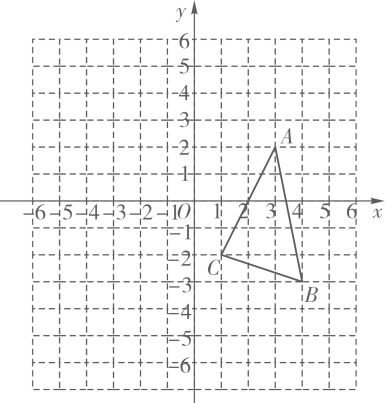
1. （1）将三角形ABC向左平移5个单位长度，再向上平移4个单位长度，得到三角形A₁B₁C₁ ，在图中画出三角形A₁B₁C₁ ，并直接写出点A₁ ， B₁ ， C₁的坐标；
2. （2）求出三角形A₁B₁C₁的面积．
答案解析收藏纠错 + 选题
20. (2023七下·岳池期中) 如图，直线AB，CD相交于点O，OF⊥OC于O，OE平分∠AOF，∠COE=15°，求∠BOD的度数．

答案解析收藏纠错 + 选题

四、实践应用题(本大题共3个小题，第21小题6分，第22、23题各8分，共22分)

21. (2023七下·岳池期中) 某小区为了促进全民健身活动的开展，决定在一块面积为100m²的正方形空地上建一个篮球场．已知篮球场的面积为540m² ，其中长是宽的 $\text{[math]}$ 倍，篮球场的四周必须留出1m宽的空地，请你通过计算说明能否按规定在这块空地上建一个篮球场？

答案解析收藏纠错 + 选题
22. (2023七下·澧县期末) 如图1是一个由齿轮、轴承、托架等元件构成的手动变速箱托架，其主要作用是动力传输．如图2是手动变速箱托架工作时某一时刻的示意图，已知AB∥CD，CG∥EF，∠BAG=150°，∠AGC=80°，求∠DEF的度数．

答案解析收藏纠错 + 选题
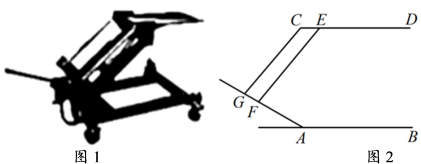
23. (2023七下·岳池期中) 阅读下面材料：．
∵ $\text{[math]}$ < $\text{[math]}$ < $\text{[math]}$ ，即2< $\text{[math]}$ <3，

∴ $\text{[math]}$ 的整数部分为2，小数部分为 $\text{[math]}$ -2．

请解答下列问题；
1. （1） $\text{[math]}$ 的整数部分是，小数部分是；
2. （2）已知7- $\text{[math]}$ 的小数部分是m，7+ $\text{[math]}$ 的小数部分是n，求m+n的值．
答案解析收藏纠错 + 选题

五、推理论证题(本大题共2个小题，每小题8分，共16分)

24. (2023七下·岳池期中) 如图，点E、F分别在AB、CD上，AF⊥CE于点O，∠l=∠B，∠A+∠2=90°，求证：AB∥CD．请完善解答过程，并在括号内填写相应的依据．

证明：∵AF⊥CE (已知)，

∴∠AOE=90° （）

又，∵∠1=∠B(已知)

∴      ▲ ∥      ▲ (同位角相等，两直线平行)，

∴∠AFB=∠AOE（）

∴∠AFB=      ▲ °，

又∵∠AFC+∠AFB+∠2=180°(平角的定义)

∴∠AFC+∠2=      ▲ °

又∵∠A+∠2=90° (已知)

∴∠A=∠AFC （）

∴AB∥CD．（    )

答案解析收藏纠错 + 选题
25. (2023七下·岳池期中) 如图，AF的延长线与BC的延长线交于点E，AD∥BE，∠1=∠2，∠3=∠4．
1. （1）求证：AB∥DC；
2. （2）若∠B=78°，∠E=25°，求∠CAE的度数．
答案解析收藏纠错 + 选题

六、拓展探索题(共10分)

26. (2023七下·岳池期中) 如图，已知AM∥BN，∠A=60°，点P是射线AM上一动点(点P与点A不重合)，BC、BD分别平分∠ABP和∠PBN．
1. （1）求∠ABN的度数；
2. （2）当点P运动时，∠CBD的度数是否随之发生变化？若不变化，请求出它的度数；若变化，请写出变化规律；
3. （3）当点P运动到使∠ACB=∠ABD时，求∠ABC的度数．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

四川省广安市岳池县2022-2023学年七年级下学期数学期中...

副标题：

*注意事项：

四川省广安市岳池县2022-2023学年七年级下学期数学期中...

试题分析

总体分析

题量分析

难度分析

知识点分析