山西省吕梁市交口县2020-2021学年七年级下学期期末数学...

更新时间：2024-07-13 浏览次数：63 类型：期末考试

一、单选题

1. (2021七下·交口期末) 下列是无理数的是（）

A . $\text{[math]}$ B . 1.414 C . $\text{[math]}$ D . 0.9

答案解析收藏纠错 + 选题
2. (2021七下·交口期末) 2022年，在中国举办了第二十四届冬季奥林匹克运动会，图中是吉祥物“冰墩墩”，将图中的“冰墩墩”通过平移可以得到的图形是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023八上·瓯海期中) 已知 $\text{[math]}$ ，则下列不等式成立的是 $\text{[math]}$ 　　 $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024八下·晋江期中) 在平面直角坐标系中，点（ $\text{[math]}$ ， $\text{[math]}$ ）所在的象限是（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
5. (2021七下·交口期末) 下列调查中，最适合采用全面调查（普查）方式的是（）

A . 调查我国最大的航天器“天和”核心舱零件的质量情况 B . 调查全国中小学生收看央视一套播出的大型公益节目《开学第一课》的收视率 C . 调查某一批LED灯的使用寿命 D . 调查我省居民进行垃圾分类的情况

答案解析收藏纠错 + 选题
6. (2021七下·交口期末) 若关于 $\text{[math]}$ ， $\text{[math]}$ 的二元一次方程 $\text{[math]}$ 的一组解为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . 2

答案解析收藏纠错 + 选题
7. (2021七下·交口期末) 如图，已知∠1+∠2＝180°，∠3＝55°，那么∠4的度数是（）

A . 35° B . 45° C . 55° D . 125°

答案解析收藏纠错 + 选题
8. (2021七下·交口期末) 用“加减法”将方程组 $\text{[math]}$ 中的x消去后得到的方程是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2021七下·交口期末) 不等式组 $\text{[math]}$ 的解集在数轴上表示为（）

A . B . C . D .

答案解析收藏纠错 + 选题
10. (2021七下·交口期末) 《九章算术》是我国东汉初年编订的一部数学经典著作，在它的“方程”里，一次方程组是由算筹布置而成的．《九章算术》中的算筹图是竖排的，为看图方便，我们把它改为横排的，如图1、图2图中各行从左到右列出的算筹分别表示未知数x，y的系数与相应的常数项．把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来，就是 $\text{[math]}$ ，类似地，图2所示的算筹图我们可以表述为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2024七下·拱墅月考) 写出一个解是 $\text{[math]}$ 的二元一次方程组：.

答案解析收藏纠错 + 选题
12. (2021七下·交口期末) 已知点P（2-a，3a）在第二象限，那么a的取值范围是．

答案解析收藏纠错 + 选题
13. (2023七下·铜仁期末) 下列三个日常现象：
其中，可以用“垂线段最短”来解释的是（填序号）．

答案解析收藏纠错 + 选题
14. (2021七下·交口期末) 为弘扬中华传统文化，某校组织八年级1000名学生参加汉字听写大赛.为了解学生整体听写能力，从中抽取部分学生的成绩（得分取正整数，满分为100分）进行统计分析，得到分数段在70.5～80.5的频数是50，所占百分比25％，则本次抽样调查的样本容量为.

答案解析收藏纠错 + 选题
15. (2021七下·交口期末) 在平面直角坐标系中，点 $\text{[math]}$ 经过某种变换后得到点 $\text{[math]}$ ，我们把点 $\text{[math]}$ 叫做点 $\text{[math]}$ 的终结点．已知点 $\text{[math]}$ 的终结点为 $\text{[math]}$ ，点 $\text{[math]}$ 的终结点为 $\text{[math]}$ ，点 $\text{[math]}$ 的终结点为 $\text{[math]}$ ，这样依次得到 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、… $\text{[math]}$ ，若点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为．

答案解析收藏纠错 + 选题

三、解答题

16. (2021七下·交口期末)
1. （1）计算： $\text{[math]}$
2. （2）解方程组： $\text{[math]}$
答案解析收藏纠错 + 选题
17. (2024七下·西岗期末) 解不等式组： $\text{[math]}$ ，并把解集在数轴上表示出来.

答案解析收藏纠错 + 选题
18. (2021七下·交口期末) 如图所示，三角形 $\text{[math]}$ 三个顶点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）三角形 $\text{[math]}$ 向左平移2个单位长度，再向上平移3个单位长度，恰好得到三角形 $\text{[math]}$ ，试写出三角形 $\text{[math]}$ 三个顶点的坐标；
2. （2）求三角形 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
19. (2021七下·交口期末) 推理填空：如图， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，试说明 $\text{[math]}$ ．
理由：∵ $\text{[math]}$ （已知），
∴ $\text{[math]}$   ▲  （   ）∴ $\text{[math]}$   ▲   ，
∵ $\text{[math]}$ （已知），∴ $\text{[math]}$   ▲   ，又∵ $\text{[math]}$ （已知），
∴ $\text{[math]}$   ▲  +  ▲  （   ），即 $\text{[math]}$   ▲   ，
∴ $\text{[math]}$ （   ）．

答案解析收藏纠错 + 选题
20. (2021七下·交口期末) 以“创新”为发展理念的中国科技取得了举世瞩目的成就，某校就下列科技：A（中国“天眼”开启地外文明搜索）、B（天问一号的升空）、C（嫦娥五号探月）、D（北斗三号全球卫星导航）最感兴趣的成就随机抽取本校部分学生进行问卷调查（每人必选且只选一项），如图是整理数据后绘制的两幅不完整的统计图．
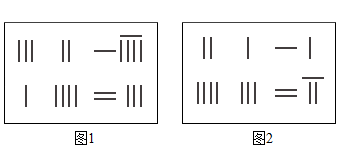
请你根据图中提供的信息回答下列问题：
1. （1）本次接受问卷调查的有 ▲ 人，并补全条形统计图；
2. （2）选项B所对应扇形圆心角为；
3. （3）估计该校2200名学生中，对选项C感兴趣的有多少名学生？
答案解析收藏纠错 + 选题

21. (2021七下·交口期末) 阅读与探究

本学期我们在第六章《实数》中，学习了平方根和立方根，下表是平方根和立方根的部分内容．

	平方根	立方根
定义	一般地，如果一个数的平方等于 $\text{[math]}$ ，那么这个数叫做 $\text{[math]}$ 的平方根或二次方根．这就是说，如果 $\text{[math]}$ ，那么 $\text{[math]}$ 叫做 $\text{[math]}$ 的平方根．	一般地，如果一个数的立方等于 $\text{[math]}$ ，那么这个数叫做 $\text{[math]}$ 的立方根或三次方根．这就是说，如果 $\text{[math]}$ ，那么 $\text{[math]}$ 叫做 $\text{[math]}$ 的立方根．
运算	求一个数 $\text{[math]}$ 的平方根的运算，叫做开平方．开平方与平方互为逆运算．	求一个数 $\text{[math]}$ 的立方根的运算，叫做开立方．开立方与立方互为逆运算．
特征	正数有两个平方根，他们互为相反数；0的平方根是0；负数没有平方根．	正数的立方根是正数，0的立方根是0；负数的立方根是负数．
表示方法	正数 $\text{[math]}$ 的平方根可以用“ $\text{[math]}$ ”表示，读作“正负根号 $\text{[math]}$ ”．	一个数 $\text{[math]}$ 的立方根可以用“ $\text{[math]}$ ” 表示，读作“三次根号 $\text{[math]}$ ”．

今天我们类比平方根和立方根的学习方法学习四次方根．

（1）探究定义：填写下表．
$\text{[math]}$
1
16
$\text{[math]}$
$\text{[math]}$
类比平方根和立方根的定义，给四次方根下定义：．
（2）探究性质：①81的四次方根是 ▲ ；0的四次方根是 ▲ ； $\text{[math]}$ ▲ （填“有”或“没有”）四次方根．
②类比平方根和立方根的性质，归纳四次方根的性质： ▲ ．
（3）在探索过程中，你用到了哪些数学思想？请写出两个：．
（4）拓展应用
① $\text{[math]}$ （将结果直接填到横线上）
②比较大小： $\text{[math]}$ $\text{[math]}$ （填“＞”、“=”或“＜”）

答案解析收藏纠错 + 选题

22. (2021七下·交口期末) 习近平总书记说：“读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然之气”，某校为提高学生的阅读品味，现决定购买《艾青诗选》和《格列佛游记》两种书，已知购买2本《艾青诗选》和1本《格列佛游记》需100元；购买6本《艾青诗选》与购买7本《格列佛游记》的价格相同．
1. （1）求这两种书的单价各多少元？
2. （2）若要购买《艾青诗选》和《格列佛游记》共50本，且购买两种书的总价不超过1600元，请问至多要购买《艾青诗选》多少本？
答案解析收藏纠错 + 选题
23. (2021七下·交口期末) 综合与实践：折纸中的数学
知识背景
我们在七年级上册第四章《几何图形初步》中探究了简单图形折叠问题，并进行了简单的计算与推理.七年级下册第五章我们学习了平行线的性质与判定，今天我们继续探究：折纸中的数学——长方形纸条的折叠与平行线.
1. （1）
  知识初探
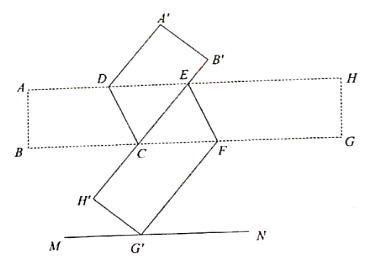
  如图1，长方形纸条 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .将长方形纸条沿直线 $\text{[math]}$ 折叠，点 $\text{[math]}$ 落在 $\text{[math]}$ 处，点 $\text{[math]}$ 落在 $\text{[math]}$ 处， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ .若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数.
2. （2）
  类比再探
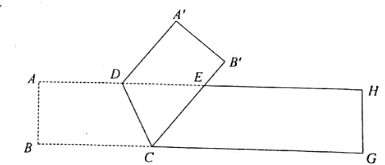
  如图2，在图1的基础上将 $\text{[math]}$ 对折，点 $\text{[math]}$ 落在直线 $\text{[math]}$ 上的 $\text{[math]}$ 处.点 $\text{[math]}$ 落在 $\text{[math]}$ 处，得到折痕 $\text{[math]}$ ，则折痕 $\text{[math]}$ 与 $\text{[math]}$ 有怎样的位置关系？说明理由.
3. （3）
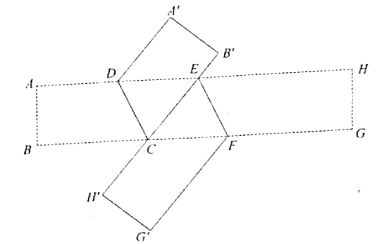
  拓展延伸
  如图3，在图2的基础上，过点 $\text{[math]}$ 作 $\text{[math]}$ 的平行线 $\text{[math]}$ ，请你猜想 $\text{[math]}$ 和 $\text{[math]}$ 的数量关系，并说明理由.
答案解析收藏纠错 + 选题