浙江省宁波市慈溪实验中学2022-2023学年九年级下学期第...

更新时间：2023-05-29 浏览次数：49 类型：月考试卷

一、单选题

1. (2023九下·慈溪月考) 下列选项中，-2的相反数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2 D . -2

答案解析收藏纠错 + 选题
2. (2024九下·漯河模拟) 下列说法正确的是（）

A . 了解一批灯泡的使用寿命，应采用抽样调查的方式 B . 如果某彩票的中奖概率是1%，那么一次购买100张这种彩票一定会中奖 C . 若甲、乙两组数据的平均数相同， $\text{[math]}$ ， $\text{[math]}$ ，则乙组数据较稳定 D . “任意掷一枚质地均匀的骰子，掷出的点数是7”是必然事件

答案解析收藏纠错 + 选题
3. (2024九上·青山期末) 将抛物线 $\text{[math]}$ 向下平移1个单位长度，再向左平移2个单位长度后，得到的抛物线表达式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023九下·慈溪月考) 下列语句中不正确的有（）
①平分弦的直径垂直于弦；②相等的圆心角所对的弧相等；③长度相等的两条弧是等弧；④圆是轴对称图形，任何一条直径都是它的对称轴；⑤圆内接四边形的对角互补.

A . 5个 B . 4个 C . 3个 D . 2个

答案解析收藏纠错 + 选题
5. (2023九下·慈溪月考) 将一个正方体截一个角，得到如图所示的几何体，则这个几何体的俯视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2023九下·慈溪月考)
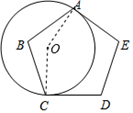
如图，直径AB，CD的夹角为60°，P为⊙O上的一个动点（不与点A，B，C，D重合）．PM，PN分别垂直于CD，AB，垂足分别为M，N．若⊙O的半径长为2，则MN的长（　　）

A . 随P点运动而变化，最大值为 $\text{[math]}$ B . 等于 $\text{[math]}$ C . 随P点运动而变化，最小值为 $\text{[math]}$ D . 随P点运动而变化，没有最值

答案解析收藏纠错 + 选题
7. (2023九下·慈溪月考) 二次函数 $\text{[math]}$ 图象 $\text{[math]}$ 经过点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，其中 $\text{[math]}$ .以下选项错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024九上·顺德期末) 如图1，已知A，B是反比例函数 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ）图象上的两点， $\text{[math]}$ 轴，交y轴于点C，动点P从坐标原点O出发，沿 $\text{[math]}$ （图中“ $\text{[math]}$ ”所示路线）匀速运动，终点为C，过P作 $\text{[math]}$ 轴，垂足为M.设三角形 $\text{[math]}$ 的面积为S，P点运动时间为t，则S关于t的函数图象大致如图2，则k的值为（）

A . 8 B . 6 C . 4 D . 2

答案解析收藏纠错 + 选题
9. (2023九下·慈溪月考) 有一块锐角三角形余料 $\text{[math]}$ ，边 $\text{[math]}$ 的长为 $\text{[math]}$ ， $\text{[math]}$ 边上的高为 $\text{[math]}$ ，现要把它分割成若干个邻边长分别为 $\text{[math]}$ 和 $\text{[math]}$ 的小长方形零件，分割方式如图所示（分割线的耗料不计），使最底层的小长方形的长为 $\text{[math]}$ 的边在 $\text{[math]}$ 上，则按如图方式分割成的小长方形零件最多有（）

A . 5个 B . 6个 C . 7个 D . 8个

答案解析收藏纠错 + 选题
10. (2023九下·慈溪月考) 如图，E，F，G，H为正方形各边中点，连接EG，FH交于点O.点P是正方形内一点，连接EP、FP、GP、HP.这四条线段把正方形分为4个部分，分别记每个区域的面积为S₁ ， S₂ ， S₃ ， S₄ ，若要求得△FPH与△EPG的面积之差，则只需知道（）

A . $\text{[math]}$ 与 $\text{[math]}$ 的面积之差 B . $\text{[math]}$ 与 $\text{[math]}$ 的面积之差 C . $\text{[math]}$ 与 $\text{[math]}$ 的面积之差 D . $\text{[math]}$ 与 $\text{[math]}$ 的面积之差

答案解析收藏纠错 + 选题

二、填空题

11. (2023九上·义乌月考) 如果 $\text{[math]}$ ，那么 $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2023九下·慈溪月考) 《九章算术》是我国东汉初年编订的一部数学经典著作，其中一次方程组是用算筹布置而成，如图（1）所示的算筹图用我们现在所熟悉的方程组表示出来，就是 $\text{[math]}$ ，类似的，图（2）所示的算筹图用方程组表示出来，就是.

答案解析收藏纠错 + 选题
13. (2023九下·慈溪月考) 在平面直角坐标系中，将点 $\text{[math]}$ 向下平移5个单位长度得到点 $\text{[math]}$ ，若点 $\text{[math]}$ 恰好在反比例函数 $\text{[math]}$ 的图象上，则 $\text{[math]}$ 的值是.

答案解析收藏纠错 + 选题
14. (2023九下·慈溪月考) 如图，⊙O与正五边形ABCDE的两边AE、CD分别相切于A、C两点，则∠AOC的度数为度.

答案解析收藏纠错 + 选题
15. (2023九下·慈溪月考) 活动探究：我们知道，已知两边和其中一边的对角对应相等的两个三角形不一定全等.如已知 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 所对的边为 $\text{[math]}$ ，满足已知条件的三角形有两个（我们发现其中如图的 $\text{[math]}$ 是一个直角三角形），则满足已知条件的三角形的第三边长为

答案解析收藏纠错 + 选题
16. (2023九下·慈溪月考) 如图，在正方形ABCD中，AB＝2 $\text{[math]}$ ，将线段CD绕点C顺时针旋转α至射线l，作点D关于射线l的对称点M，连接BM交直线l于点N，当α＝°时，线段AN取得最大值；线段AN的最大值为.

答案解析收藏纠错 + 选题

三、解答题

17. (2023九下·慈溪月考)
1. （1）计算： $\text{[math]}$ ；
2. （2）解不等式组 $\text{[math]}$ ，并将其解集在数轴上表示出来.
答案解析收藏纠错 + 选题
18. (2023九下·慈溪月考) 在6×8的正方形网格，每个小正方形的顶点称为格点，已知线段AB，其中点A在直线MN上.请用无刻度的直尺按要求作图，保留作图痕迹.
1. （1）在图①中，在直线MN上找到一点C，作△ABC，使得∠ACB＝45°；
2. （2）在图②中，在直线MN上找到一点D，作△ABD，使得∠ABD＝45°；
3. （3）在图③中，在直线MN上找到一点E，作△ABE，使得∠EAB＝∠EBA.
答案解析收藏纠错 + 选题
19. (2023九下·慈溪月考) 某校随机抽取九年级部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动，学校收集整理数据后，将减压方式分为五类，并绘制了图1、图2两个不完整的统计图，请根据图中的信息解答下列问题：
1. （1）九年级接受调查的同学共有多少名，并补全条形统计图；
2. （2）九年级共有500名学生，请你估计该校九年级听音乐减压的学生有多少名；
3. （3）若喜欢“交流谈心”的5名同学中有三名男生和两名女生，心理老师想从5名同学中任选两名同学进行交流，请直接写出同时选出的两名同学都是女生的概率.
答案解析收藏纠错 + 选题
20. (2023九下·慈溪月考) 已知抛物线 $\text{[math]}$ （b是常数）经过点 $\text{[math]}$ .
1. （1）求该抛物线解析式；
2. （2）直接写出当 $\text{[math]}$ 时，y的取值范围.
3. （3）若 $\text{[math]}$ 为抛物线上的一个动点，P关于原点的对称点为 $\text{[math]}$ ，当点 $\text{[math]}$ 落在该抛物线上时，求m的值.
答案解析收藏纠错 + 选题
21. (2023九下·慈溪月考) 图①是某车站的一组智能通道闸机，当行人通过时智能闸机会自动识别行人身份，识别成功后，两侧的圆弧翼闸会收回到两侧闸机箱内，这时行人即可通过．图②是两圆弧翼展开时的截面图，扇形 $\text{[math]}$ 和 $\text{[math]}$ 是闸机的“圆弧翼”，两圆弧翼成轴对称， $\text{[math]}$ 和 $\text{[math]}$ 均垂直于地面，扇形的圆心角 $\text{[math]}$ ，半径 $\text{[math]}$ ，点 $\text{[math]}$ 与点 $\text{[math]}$ 在同一水平线上，且它们之间的距离为 $\text{[math]}$ ．
1. （1）求闸机通道的宽度，即 $\text{[math]}$ 与 $\text{[math]}$ 之间的距离（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）；
2. （2）经实践调查，一个智能闸机的平均检票速度是一个人工检票口平均检票速度的 $\text{[math]}$ 倍， $\text{[math]}$ 人的团队通过一个智能闸机口比通过一个人工检票口可节约 $\text{[math]}$ 分钟，求一个智能闸机平均每分钟检票通过的人数．
答案解析收藏纠错 + 选题
22. (2023九下·慈溪月考) 已知A，B两地之间有一条长240千米的公路.甲车从A地出发匀速开往B地，甲车出发半小时后，乙车从A地出发沿同一路线匀速追赶甲车，两车相遇后，乙车原路原速返回A地.两车之间的距离y（千米）与甲车行驶时间x（小时）之间的函数关系如图所示，请解答下列问题：
1. （1）甲车的速度是千米/时，乙车的速度是千米/时，m＝.
2. （2）求乙车返回过程中，y与x之间的函数关系式.
3. （3）当甲、乙两车相距160千米时，直接写出甲车的行驶时间.
答案解析收藏纠错 + 选题
23. (2023九下·慈溪月考) 如图
【方法尝试】如图1，矩形 $\text{[math]}$ 是矩形 $\text{[math]}$ 以点A为旋转中心，按逆时针方向旋转 $\text{[math]}$ 所得的图形， $\text{[math]}$ 分别是它们的对角线.求证： $\text{[math]}$ .
【类比迁移】如图2，在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .将 $\text{[math]}$ 绕点 $\text{[math]}$ 在平面内逆时针旋转，设旋转角 $\text{[math]}$ 为 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ .
①请判断线段 $\text{[math]}$ 和 $\text{[math]}$ 的数量关系和位置关系，并说明理由；
②当点B，D，E在同一直线上时，求线段 $\text{[math]}$ 的长.
【拓展延伸】如图3，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ，在射线 $\text{[math]}$ 上取一点 $\text{[math]}$ ，连接 $\text{[math]}$ ，使得 $\text{[math]}$ ，请直接写出线段 $\text{[math]}$ 的最值.

答案解析收藏纠错 + 选题
24. (2023九下·慈溪月考) 如图，等腰 $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ，过点B作 $\text{[math]}$ 的垂线，交 $\text{[math]}$ 于点D，交 $\text{[math]}$ 于点M，交 $\text{[math]}$ 于点E，连接 $\text{[math]}$ .
1. （1）若 $\text{[math]}$ ，请用含α的代数式表示 $\text{[math]}$ ；
2. （2）求证： $\text{[math]}$ ；
3. （3）连接 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的值及四边形 $\text{[math]}$ 的面积与 $\text{[math]}$ 面积的比值.
答案解析收藏纠错 + 选题