一、选择题(本大题共10小题，每小题3分，共30分．在每小题给出的选项中，只有一项是符合题目要求的)
-
-
-
A . x1=2，x2=-6
B . x1=-2，x2=6
C . x1=-2，x2=-6
D . x1=2，x2=6
-
4.
(2023·广东模拟)
一次函数y=kx+b满足kb>0，且y随x的增大减小，则此函数的图象不经过（ ）
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
-
A . 线段PA的长度
B . 线段PB的长度
C . 线段PC的长度
D . 线段PD的长度
-
A . m+2>n+2
B . 2m>2n
C . 
D . m2>n2
-
-
A . 钝角三角形
B . 锐角三角形
C . 直角三角形
D . 等边三角形
-
9.
(2023·广东模拟)
如图，在平面直角坐标系中，将
以原点O为位似中心放大后得到
，若
，
，则
与
的相似比是（ ）
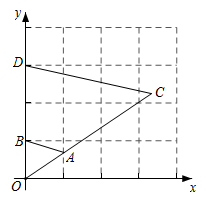
A . 2：1
B . 1：2
C . 3：1
D . 1：3
-
10.
(2023·广东模拟)
已知抛物线y=ax
2+bx+c(a，b，c是常数，a≠0)经过点(-1，-1)，(0，1)，当x=-2时，与其相对应的函数值y>1．有下列结论：
①abc>0；
②关于x的方程ax2+bx+c-3= 0有两个不相等的实数根；
③a+b+c>7；
其中，正确结论的个数是（ ）
A . 0
B . 1
C . 2
D . 3
二、填空题(本大题共5小题，每小题3分，共15分．请把答案填在答题卡相应位置上)
三、解答题(本大题共3小题，每小题8分，共24分)
-
-
17.
(2023·广东模拟)
老师在黑板上写了一个正确的演算过程，随后用手掌捂住了一部分多项式，形式如下：
+(a+b)2=2a2+6b2
-
-
（2）
当a=-2，b=
时，求所捂的多项式的值．
-
18.
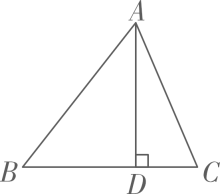
(2023·广东模拟)
如图，在△ABC中，AD⊥BC ，垂足是点D，若BC=14，AD=12，tan∠BAD=
， 求sinC的值．
四、解答题(本大题共3小题，每小题9分，共27分)
-
19.
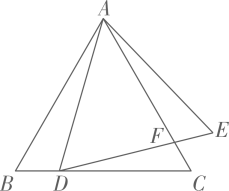
(2023·广东模拟)
如图，点D在等边AABC的BC边上，△ADE为等边三角形，DE与AC交于点F．
-
-
（2）
除了△ABD△DCF外，请写出图中其他所有的相似三角形．
-
20.
(2023·广东模拟)
在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩(单位：m)，绘制出如下的统计图1和统计图2．请根据相关信息，解答下列问题：
-
-
（2）
求统计的这组初赛成绩数据的平均数、众数和中位数；
-
（3）
根据这组初赛成绩，由高到低确定9人能进入复赛，请直接写出初赛成绩为1.65m的运动员能否进入复赛．
-
21.
(2023·广东模拟)
为了防疫需要，某医院现决定购买一批防护服，已知甲、乙两种型号的防护服的单价分别是310元和460元，且每种型号的防护服必须整套购买．
-
（1）
若购买甲、乙两种型号的防护服共100套，且恰好支出40000元，求甲、乙两种型号的防护服各购买了多少套？
-
（2）
若购买甲、乙两种型号的防护服共100套，且支出不超过36000元，求甲种型号的防护服至少要购买多少套？
五、解答题三(本大题共2小题，每小题12分，共24分)
-
22.
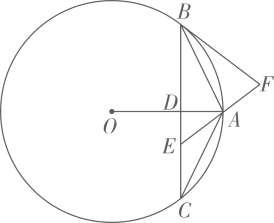
(2023·广东模拟)
如图，在⊙O中，半径OA垂直弦BC于点D，点E在CD上，使△EAC∽△ABC．点F在EA的延长线上，连接FB，且FE=FB．
-
-
-
（3）
若AD=10，tanC=
， 求EF的长．
-
23.
(2023·广东模拟)
抛物线y=ax
2+c与x轴交于A、B两点，顶点为C，点P在抛物线上，且位于x轴下方．
-
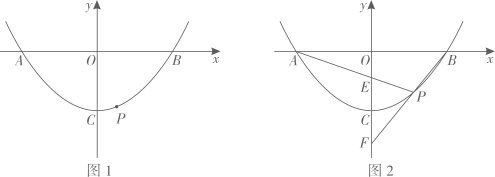
（1）
如图1，若P(1，-3)，B(4，0)．
①求该抛物线的解析式；
②若D是抛物线上一点，满足∠DPO=∠POB，求点D的坐标；
-
（2）
如图2，已知直线PA，PB与y轴分别交于E，F两点，当点P运动时，
是否为定值？若是，试求出该定值；若不是，请说明理由．
B . 
C . 
D . 
+(a+b)2=2a2+6b2
