一、单选题(本大题共12小题,每小题3分,共36分)
-
-
-
A . 2,3,4
B . 5,12,13
C . 4,6,8
D . 5,12,15
-
-
5.
(2023八下·南宁月考)
某中学四名跳远运动员在10次跳远测试中成绩的平均数相同,方差分别是

,

,

,

, 要选出一名跳远成绩最稳定的选手参加市中学生运动会,应选择的选手是( )
A . 甲
B . 乙
C . 丙
D . 丁
-
6.
菱形具有而矩形不一定具有的性质是( )
A . 对边平行
B . 对角线互相平分
C . 对角线互相垂直
D . 对角互补
-
A . 一组对边平行,另一组对边相等的四边形是平行四边形
B . 对角线相等的平行四边形是矩形
C . 一个角为 且一组邻边相等的四边形是正方形
D . 对角线互相垂直的四边形是菱形
且一组邻边相等的四边形是正方形
D . 对角线互相垂直的四边形是菱形
-
-
9.
(2023八下·南宁月考)
费尔兹奖是国际上享有崇高声誉的一个数学奖项,每四年评选一次,主要授予年轻的数学家.下面数据是部分获奖者获奖时的年龄(单位:岁):35,32,35,40,33,29,则这组数据的众数和中位数分别是( )
A . 35,35
B . 35,33
C . 34,35
D . 35,34
-
10.
(2023八下·南宁月考)
我国明代有一位杰出的数学家提出一道“荡秋千”的数学问题:“平地秋千未起,踏板一尺离地,送行二步与人齐,五尺人高曾记;仕女佳人争蹴,终朝笑语欢嬉,良工高士素好奇,算出索长有几?”其意思为:如图所示,当秋千静止在地面上时,秋千的踏板离地的距离为一尺(

尺),将秋千的踏板往前推两步(每一步合五尺,即

尺),秋千的踏板与人一样高,这个人的身高为五尺(

尺),求这个秋千的绳索

有多长?( )

A . 12尺
B .  尺
C .
尺
C .  尺
D .
尺
D .  尺
尺
-
-
二、填空题(本大题共6小题,每小题2分,共12分)
-
-
14.
(2024八下·德惠期末)
小明参加“强国有我”主题演讲比赛,其演讲形象、内容、效果三项的成绩分别是

分、

分、

分.若将三项得分依次按

的比例确定最终成绩,则小明的最终比赛成绩为
分.
-
-
-
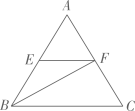
17.
(2023八下·徐汇期末)
如图,在△ABC中,E、F分别是AB、AC的中点,若BF平分∠ABC,BC=6,则BE的长为
.
-
18.
(2023八下·南宁月考)
如图,在

中,

,

, 点

在直线

上,

, 点

为

上一动点,连接

,

. 当

的值最小时,

的度数为
度.

三、解答题(本大题共8小题,共72分)
-
-
-
-
(1)
尺规作图:作

的垂直平分线,交

于点

(不写做法,保留作图痕迹);
-
(2)
连接

, 求
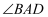
的度数.
-
22.
(2023八下·南宁月考)
为了解某校九年级学生的理化生实验操作情况,随机抽查了若干名学生的实验操作得分(满分为10分),根据获取的样本数据,制作了如图的统计图(1)和图(2),请根据相关信息,解答下列问题:

-
(1)
本次随机抽查的学生人数为
,在图(2)中,“①”的描述应为“7分

”,其中m的值为
;
-
(2)
抽取的学生实验操作得分数据的平均数为分,众数为分,中位数为分;
-
(3)
若该校九年级共有1280名学生,估计该校理化生实验操作得满分的学生有多少人?
-
-
(1)
四边形

是平行四边形
-
(2)

.
-
24.
(2023八下·阳西期末)
近日,我校正在创建全国的“花香校园”.为了进一步美化校园,我校计划购买A,B两种花卉装点校道,学校负责人到花卉基地调查发现:购买2盆A种花和1盆B种花需要13元,购买3盆A种花和2盆B种花需要22元.
-
-
(2)
学校若购买A,B两种花共1000盆,设购买的B种花m盆

, 总费用为

元,请你帮公司设计一种购花方案,使总花费最少,并求出最少费用为多少元?
-
-
(1)
求直线

的函数解析式;
-
(2)
在直线

上是否存在点P,使得

的面积是

的面积的2倍?如果存在,请求出P坐标;如果不存在,请说明理由.
-
-
(1)
【感知】
如图1,若点P是边 的中点,小南经过探索发现了线段
的中点,小南经过探索发现了线段 与
与 之间的数量关系,请你写出这个关系式.
之间的数量关系,请你写出这个关系式.
-
(2)
【探究】
如图2,小阳说“点P为 上任意一点时,(1)中的结论仍然成立”,你同意吗?请说明理由.
上任意一点时,(1)中的结论仍然成立”,你同意吗?请说明理由.
-
 B .
B .  C .
C .  D .
D . 



的中点,小南经过探索发现了线段
与
之间的数量关系,请你写出这个关系式.
上任意一点时,(1)中的结论仍然成立”,你同意吗?请说明理由.
, 测得
,
, 在
边上取一点P,连接
, 在菱形内部作
,
交
于点Q,当
时,请直接写出线段
的长.