吉林省长春市榆树市八号镇2022-2023学年七年级下学期7...

更新时间：2024-07-14 浏览次数：44 类型：期末考试

一、选择题（每题3分，共24分）

1. (2023七下·榆树期末) 若x²＝4，则x的值是（）

A . 2 B . ±2 C . 16 D . ±16

答案解析收藏纠错 + 选题
2. (2023七下·榆树期末) 在平面直角坐标系中，点P（-1，x²+1）（其中x为任意有理数）一定在（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
3. (2023七下·榆树期末) 下列数中 $\text{[math]}$ ， 0.101001， $\text{[math]}$ ， $\text{[math]}$ ，无理数是（）

A . $\text{[math]}$ B . 0.101001 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023七下·榆树期末) 不等式-2x+1＜3的解集是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2023七下·榆树期末) 我国明代数学读本《算法统宗》一书有这样一道题：一支竿子一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托。如果1托为5尺，那么索长和竿子长分别为多少尺？设索长为x尺，竿子长为y尺，可列方程组为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023七下·榆树期末) 下列图标既不是轴对称图形也不是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2023七下·榆树期末) 如图，AC∥ED，∠C＝26°，∠B＝37°，则∠E的大小是（）

A . 53° B . 63° C . 73° D . 83

答案解析收藏纠错 + 选题
8. (2023七下·榆树期末) 如图，在△ABC中，∠ACB＝90°，∠BAC＝α，将△ABC绕点C顺时针旋转90°得到△A'B'C，点B的对应点B'在边AC上（不与点A，C重合），则∠AA'B'的度数为（）

A . α B . α-45° C . 45°-α D . 90°-α

答案解析收藏纠错 + 选题

二、填空题（每题3分，共18分）

9. (2024六上·闵行期中) $\text{[math]}$ ＝．

答案解析收藏纠错 + 选题
10. (2023七下·榆树期末) 不等式2x+4≤0的解集为．

答案解析收藏纠错 + 选题
11. (2023七下·榆树期末) $\text{[math]}$ 是关于x和y的二元一次方程ax+y＝1的解，则a的值为．

答案解析收藏纠错 + 选题
12. (2023七下·渭滨期末) 如图，在灌溉时，要把河中的水引到农田 $\text{[math]}$ 处，并要求所挖的渠道最短，小明画线段 $\text{[math]}$ ，他的根据是.

答案解析收藏纠错 + 选题
13. (2023七下·榆树期末) 如图所示的图案，至少要绕图案中心点旋转度后，才能与原来的图形重合．

答案解析收藏纠错 + 选题
14. (2023七下·榆树期末) 如图，将矩形ABCD沿AE向上折叠，使点B落在DC边上的F处，若△AFD的周长为9，△ECF的周长为3，则矩形ABCD的周长为．

答案解析收藏纠错 + 选题

三、解答题（78分）

15. (2023七下·榆树期末) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2023七下·榆树期末) 解方程组： $\text{[math]}$

答案解析收藏纠错 + 选题
17. (2023七下·榆树期末) 解不等式： $\text{[math]}$ ，并把解集在数轴上表示出来．

答案解析收藏纠错 + 选题
18. (2023七下·榆树期末) 被誉为“最美高铁”的长春至珲春城际铁路途经许多隧道和桥梁，其中隧道累计长度与桥梁累计长度之和为342km，隧道累计长度的2倍比桥梁累计长度多36km．求隧道累计长度与桥梁累计长度．

答案解析收藏纠错 + 选题
19. (2023七下·榆树期末) 利用平方根的意义求方程（x-1）²＝4中x的值．

答案解析收藏纠错 + 选题
20. (2023七下·榆树期末) 如图，在△ABC中，∠AED＝80°，BD是∠ABC的平分线，DE∥BC，求∠EDB的度数．

答案解析收藏纠错 + 选题
21. (2023七下·榆树期末) 图①、图②、图③均是 $\text{[math]}$ 的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点，点A、B、C均为格点．只用无刻度的直尺，分别在给定的网格中按下列要求作图，并保留必要的画图痕迹．
1. （1）在图①中画出 $\text{[math]}$ 关于直线l对称的图形．
2. （2）在图②中画出 $\text{[math]}$ 关于点O成中心对称的图形．
3. （3）在图③中，过点C画 $\text{[math]}$ 的垂线．
答案解析收藏纠错 + 选题
22. (2023七下·榆树期末) 对于下列问题，在解答过程的空白处填上适当的内容（理由或数学式）．
如图，在直角△ABC中，CD是斜边AB上的高，∠BCD＝35°．
1. （1）求∠EBC的度数；
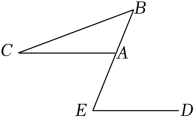
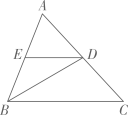
  解：∵CD⊥AB（已知），
  
  ∴∠CDB＝      ▲            °．
  
  ∵∠EBC＝∠CDB+∠BCD（    ）．
  
  ∴∠EBC＝      ▲            °+35°＝      ▲            °（等量代换）．
2. （2）求∠A的度数．
  ∵∠EBC＝∠A+∠ACB（），
  ∴∠A＝∠EBC-∠ACB（等式的性质）．
  
  ∵∠ACB＝90°（已知），
  
  ∴∠A＝ ▲ -90°＝ ▲ °（等量代换）．
答案解析收藏纠错 + 选题
23. (2023七下·榆树期末) 如图，在△ABC中，点D是BC边上的一点，∠B＝50°，∠BAD＝30°，将△ABD沿AD折叠得到△AED，AE与BC交于点F．
1. （1）求∠AFC的度数；
2. （2）求∠EDF的度数．
答案解析收藏纠错 + 选题
24. (2023七下·榆树期末) 我们在数学学习中，经常利用“转化”的思想方法解决问题，比如，我们通过“消元的方法将二元一次方程组转化为一元一次方程，从而求解．下面我们就利用“转化”的思想方法尝试解决新的问题．
先阅读下面的例题，再按要求完成下列问题．
例：解不等式（x-2）（x+1）＞0．
解：由有理数的乘法法则“两数相乘，同号得正”，得① $\text{[math]}$ 或② $\text{[math]}$
解不等式组①，得x＞2．
解不等式组②，得x＜-1．
所以不等式（x-2）（x+1）＞0的解集为x＞2或x＜-1．
根据例题方法解决下面问题：
1. （1）解不等式（x+3）（2x-1）＜0．
  解：由有理数的乘法法则“两数相乘，异号得负”，得① $\text{[math]}$ 或②．
  解不等式组①，得．
  解不等式组②，得．
  所以不等式（x+3）（2x-1）＜0的解集为．
2. （2）应用：不等式： $\text{[math]}$ 的解集为．
答案解析收藏纠错 + 选题
25. (2023七下·榆树期末) 如图，在平面直角坐标系中，已知A（0，a），B（b，0），C（3，c）三点，其中a、b、c满足关系式：|a-2|+（b-3）²+ $\text{[math]}$ ＝0．
1. （1）求a、b、c的值；
2. （2）如果在第二象限内有一点P（m， $\text{[math]}$ ），请用含m的式子表示四边形ABOP的面积；
3. （3）在（2）的条件下，是否存在负整数m，使四边形ABOP的面积不小于△AOP面积的两倍？若存在，求出所有满足条件的点P的坐标，若不存在，请说明理由．
答案解析收藏纠错 + 选题