广西壮族自治区来宾市2022-2023学年七年级下册数学期末...

更新时间：2024-07-14 浏览次数：61 类型：期末考试

一、选择题：本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项符合题目要求．

1. (2023七下·南宁期末) 下列垃圾分类图标中，是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024七下·北海期末) 下列方程组中，是二元一次方程组的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023七下·南宁期末) 一组数据3，1，3，5，4，3的众数是（）

A . 1 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
4. (2023七下·南宁期末) 下列计算中，正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023七下·来宾期末) 如图，已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023七下·南宁期末) 多项式 $\text{[math]}$ 中各项的公因式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023七下·来宾期末) 已知 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 1 B . 2 C . －1 D . －2

答案解析收藏纠错 + 选题
8. (2023七下·来宾期末) 如图，直线 $\text{[math]}$ 被直线 $\text{[math]}$ 所裁，下列说法中不正确的是（）

A . $\text{[math]}$ 与 $\text{[math]}$ 是对顶角 B . $\text{[math]}$ 与 $\text{[math]}$ 是同位角 C . $\text{[math]}$ 与 $\text{[math]}$ 是同旁内角 D . $\text{[math]}$ 与 $\text{[math]}$ 是内错角

答案解析收藏纠错 + 选题
9. (2023七下·南宁期末) 有下列现象：①高层公寓电梯的上升：②传送带的移动；③方向盘的转动；④风车的转动；⑤钟摆的运动；⑥荡秋千运动．其中属于旋转的有（）

A . 2个 B . 3个 C . 4个 D . 5个

答案解析收藏纠错 + 选题
10. (2023七下·来宾期末) 如图，三角形 $\text{[math]}$ 是由三角形 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 后得到的图形，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2023七下·来宾期末) 如图，是利用割补法求图形面积的示意图，下列公式与之相对应的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2023七下·来宾期末) 4月23日为世界读书日，某校开展了“诵读经典”系列读书活动．小明3天阅读的总页数比小红5天阅读的总页数少6页，小红平均每天阅读的页数比小明平均每天阅读的页数的2倍少10页，设小明、小红平均每天分别阅读 $\text{[math]}$ 页、 $\text{[math]}$ 页，则下列方程组正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题：本大题共6小题，每小题3分，共18分．

13. (2024八上·重庆市期中) 因式分解： $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. (2023七下·来宾期末) 把方程 $\text{[math]}$ 化成含有 $\text{[math]}$ 的代数式表示 $\text{[math]}$ 的形式： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2023七下·来宾期末) 甲、乙两位同学10次数学测试的成绩的平均分是相同的，甲同学成绩的方差为 $\text{[math]}$ ，乙同学成绩的方差为 $\text{[math]}$ ，则两位同学的数学测试成绩比较稳定的是．（填“甲”或“乙”）

答案解析收藏纠错 + 选题
16. (2023七下·南宁期末) 已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2023七下·南宁期末) 已知一组数据90，81，79，93，80，x，85，79，75，74的平均数为82，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2023七下·南宁期末) 如图，将长方形 $\text{[math]}$ 纸片沿着 $\text{[math]}$ 折叠，点 $\text{[math]}$ 和点 $\text{[math]}$ 的像分别为点 $\text{[math]}$ 和点 $\text{[math]}$ ．当 $\text{[math]}$ 时， $\text{[math]}$ 的度数为°．

答案解析收藏纠错 + 选题

三、解答题：本大题共8小题，共66分．解答应写出文字说明、证明过程或演算步骤．

19. (2023七下·南宁期末)
1. （1）计算： $\text{[math]}$ ；
2. （2）因式分解： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2023七下·来宾期末) 已知：如图，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上， $\text{[math]}$ 于点D， $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．

求证： $\text{[math]}$ ．

证明： $\text{[math]}$ 于D， $\text{[math]}$ 于 $\text{[math]}$ （已知），

∴ ▲ ∥ ▲ （在同一平面内，垂直于同一条直线的两直线平行），

∴ $\text{[math]}$ （），

∵ $\text{[math]}$ （已知），

∴ $\text{[math]}$ （），

∴ $\text{[math]}$ （），

∴ $\text{[math]}$ （）

答案解析收藏纠错 + 选题
21. (2023八上·榆林月考) 若 $\text{[math]}$ 和 $\text{[math]}$ 都是关于 $\text{[math]}$ 的二元一次方程 $\text{[math]}$ 的解，求 $\text{[math]}$ 与 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题

22. (2023七下·来宾期末) 甲、乙两名队员参加射击训练，射击次数相同，成绩分别绘制成两个统计图：

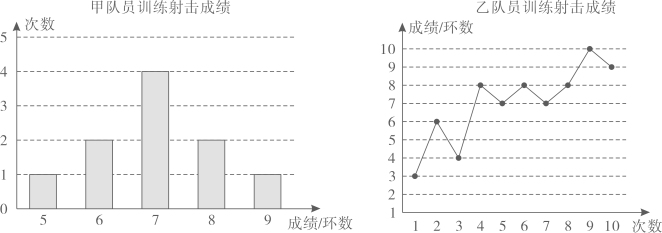
根据以上信息，整理分析数据如表：

平均成绩/环

中位数/环

众数/环

方差

甲

$\text{[math]}$

1.2

乙

$\text{[math]}$

（1）求出表格中 $\text{[math]}$ 的值；
（2）分别运用表中的四个统计量，简要分析这两名队员的射击成绩．若选派其中一名队员参赛，且鼓励参赛队员冲击最好成绩，你认为应选珢名队员？

答案解析收藏纠错 + 选题

23. (2023七下·来宾期末) 如图，在边长为1个单位长度的小正方形组成的网格中，三角形 $\text{[math]}$ 的三个顶点 $\text{[math]}$ 均在格点上，请按要求完成下列作图．

⑴作出三角形 $\text{[math]}$ 绕着 $\text{[math]}$ 点逆时针旋转 $\text{[math]}$ 得到的三角形 $\text{[math]}$ ．

⑵作出三角形 $\text{[math]}$ 关于直线 $\text{[math]}$ 对称的三角形 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
24. (2023七下·来宾期末) 如图，已知点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，射线 $\text{[math]}$ 交直线 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
2. （2）若 $\text{[math]}$ ，且 $\text{[math]}$ ，求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
25. (2023七下·来宾期末) 在“五一”黄金周期间，小明、小亮等同学随家人一同到风景区游玩，收费标准是：成人35元/张，学生票按成人票五折优惠，团体票（16人以上含16人）按成人票6折优惠．下面是购票时小明与他爸爸的对话．爸爸：大人门票每张35元学生门票对折优惠，我们共有12人，共需350元．小明：爸爸，等一下，让我算算，换一种方式买票是否可以更省钱．
1. （1）小明他们一共去了几个成人？几个学生？
2. （2）请你算算，用哪种方式买票更省钱？能省多少钱？说明理由．
答案解析收藏纠错 + 选题
26. (2023七下·来宾期末) 已知：直线 $\text{[math]}$ ，点 $\text{[math]}$ 和点 $\text{[math]}$ 是直线 $\text{[math]}$ 上的点，点 $\text{[math]}$ 和点 $\text{[math]}$ 是直线 $\text{[math]}$ 上的点，连接 $\text{[math]}$ ， $\text{[math]}$ ，设直线 $\text{[math]}$ 和 $\text{[math]}$ 交于点 $\text{[math]}$ ．
1. （1）在如图1所示的情形下，若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数（提示：可过点 $\text{[math]}$ 作 $\text{[math]}$ ；
2. （2）在如图2所示的情形下，若 $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，且 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，当 $\text{[math]}$ ， $\text{[math]}$ 时，求 $\text{[math]}$ 的度数．
3. （3）如图3，当点 $\text{[math]}$ 在点 $\text{[math]}$ 的右侧时，若 $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ，设 $\text{[math]}$ ， $\text{[math]}$ ，用含有 $\text{[math]}$ 的代数式表示 $\text{[math]}$ 的补角．（直接写出结果即可）
答案解析收藏纠错 + 选题