①求函数的图像的对称轴;
②函数的图像是否经过某两个定点?若经过某两个定点,求出这两个定点的坐标;否则,请说明理由;
如图1,在正方形中,对角线
相交于点O.在线段
上任取一点P(端点除外),连接
.
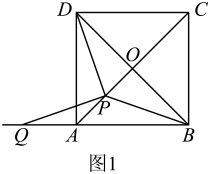
①求证:;
②将线段绕点P逆时针旋转,使点D落在
的延长线上的点Q处.当点P在线段
上的位置发生变化时,
的大小是否发生变化?请说明理由;
③探究与
的数量关系,并说明理由.
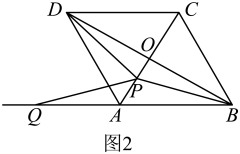
如图2,将正方形换成菱形
, 且
, 其他条件不变.试探究
与
的数量关系,并说明理由.