安徽省三海学地教育联盟2022-2023学年九年级上学期开年...

更新时间：2023-09-15 浏览次数：42 类型：开学考试

一、单选题

1. (2022九上·安徽开学考) 下列实数中，最小的数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022九上·安徽开学考) 据统计，安徽省2023年硕士研究生考试报名人数为 $\text{[math]}$ 人，其中 $\text{[math]}$ 用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022九上·安徽开学考) 已知 $\text{[math]}$ ，则a的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 0 D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022九上·安徽开学考) 2022年北京冬奥会的火炬写有全世界名字的正六边形雪花引导牌（如图① $\text{[math]}$ 共同构成的．如图②是其中一片雪花引导牌，已知点 $\text{[math]}$ 是正六边形 $\text{[math]}$ 的边 $\text{[math]}$ ， $\text{[math]}$ 的延长线的交点，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022九上·安徽开学考) 小明早上8点从家骑车去图书馆，计划在上午11点30分到达图书馆．出发半小时后，小明发现若原速骑行，将迟到10分钟，于是他加速继续骑行，平均每小时多骑行1千米，恰好准时到达，则小明原来的速度是（）

A . 12千米/小时 B . 17千米/小时 C . 18千米/小时 D . 20千米/小时

答案解析收藏纠错 + 选题
6. (2022九上·安徽开学考) 如图是由16个边长为1的小正方形组成的图形，已经有3个小正方形被涂色，在涂色一个小正方形，使它和已知阴影部分组成一个轴对称图形的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022九上·安徽开学考) 如图，在平行四边形 $\text{[math]}$ 中，E为 $\text{[math]}$ 边上的点，若 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于F，则 $\text{[math]}$ 等于（）

A . 1：9 B . 9：61 C . 9：110 D . 7：49

答案解析收藏纠错 + 选题
8. (2024九下·兴化模拟) 已知实数 $\text{[math]}$ 满足 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022九上·安徽开学考) 如图，已知点 $\text{[math]}$ 均在 $\text{[math]}$ 上， $\text{[math]}$ 为 $\text{[math]}$ 的直径，弦 $\text{[math]}$ 的延长线与弦 $\text{[math]}$ 的延长线交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．则下列命题为假命题的是（）

A . 若点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，则 $\text{[math]}$ B . 若 $\text{[math]}$ ，则 $\text{[math]}$ C . 若 $\text{[math]}$ ，则 $\text{[math]}$ D . 若半径 $\text{[math]}$ 平分弦 $\text{[math]}$ ，则四边形 $\text{[math]}$ 是平行四边形

答案解析收藏纠错 + 选题
10. (2022九上·安徽开学考) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，以每秒1个单位的速度沿着 $\text{[math]}$ 运动，同时点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，以每秒2个单位的速度沿着 $\text{[math]}$ 运动，其中一点到达终点，另一点也停止运动，设 $\text{[math]}$ ，时间为 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数图象大致为 $\text{[math]}$ $\text{[math]}$

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

11. (2022九上·安徽开学考) 在平面直角坐标系中， $\text{[math]}$ 为坐标原点，点 $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且满足 $\text{[math]}$ ．若 $\text{[math]}$ 的面积为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（在算出的结果内任选一个）．

答案解析收藏纠错 + 选题
12. (2022九上·安徽开学考) 如图，在梯形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 且 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2022九上·安徽开学考) 双曲线 $\text{[math]}$ 和 $\text{[math]}$ 如图所示，点 $\text{[math]}$ 是 $\text{[math]}$ 上一点，分别过点 $\text{[math]}$ 作 $\text{[math]}$ 轴， $\text{[math]}$ 轴，垂足分别为点 $\text{[math]}$ 、点 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 分别交于点 $\text{[math]}$ 、点 $\text{[math]}$ ，若四边形 $\text{[math]}$ 的面积为4，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
14. (2022九上·安徽开学考) 已知抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ ．
1. （1） $\text{[math]}$ 和 $\text{[math]}$ 的代数关系为；
2. （2）若 $\text{[math]}$ ，过点 $\text{[math]}$ 作直线 $\text{[math]}$ 轴，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ， $\text{[math]}$ 与抛物线交于另一点 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为直线 $\text{[math]}$ 上方抛物线上一点，求点 $\text{[math]}$ 到直线 $\text{[math]}$ 距离的最大值为．
答案解析收藏纠错 + 选题

三、解答题

15. (2022九上·安徽开学考) 解方程： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2022九上·安徽开学考) 我国古代数学著作《九章算术》中记载以下问题：今有凫起南海，七日至北海；雁起北海，九日至南海，今凫雁俱起，问何日相逢？意思是：野鸭从南海起飞，7天飞到北海；大雁从北海起飞，9天飞到南海，野鸭与大雁从南海和北海同时起飞，经过几天相遇？请解决上述问题．

答案解析收藏纠错 + 选题
17. (2022九上·安徽开学考) 观察以下等式：
第1个等式： $\text{[math]}$ ；第2个等式： $\text{[math]}$ ；
第3个等式： $\text{[math]}$ ；第4个等式： $\text{[math]}$ ； $\text{[math]}$
按照以上规律，解决下列问题：
1. （1）写出第5个等式：；
2. （2）写出你猜想的第 $\text{[math]}$ 个等式： ▲ （用含 $\text{[math]}$ 的等式表示），并证明．
答案解析收藏纠错 + 选题
18. (2022九上·安徽开学考) 如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点 $\text{[math]}$ （顶点是网格线的交点）．

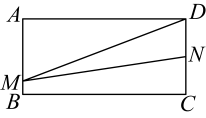
⑴以点 $\text{[math]}$ 为位似中心，在网格中画出 $\text{[math]}$ ，使 $\text{[math]}$ 与 $\text{[math]}$ 的位似比为 $\text{[math]}$ ；
⑵将 $\text{[math]}$ 向右平移7格，再向下平移2格，得到 $\text{[math]}$ ，画出 $\text{[math]}$ ；
⑶借助网格，在 $\text{[math]}$ 上选一点 $\text{[math]}$ ，使得 $\text{[math]}$ 平分 $\text{[math]}$ 的面积（保留确定关键点的画法），画出线段 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2022九上·安徽开学考) 如图是8个台阶的示意图，每个台阶的高和宽分别是1和2，每个台阶凸出的角的顶点记作 $\text{[math]}$ 为 $\text{[math]}$ 的整数）．反比例函数 $\text{[math]}$ 的图象为曲线 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ 过点 $\text{[math]}$ ，求反比例函数的解析式；
2. （2）若 $\text{[math]}$ 过点 $\text{[math]}$ ，则它必定还过另一点 $\text{[math]}$ ，求 $\text{[math]}$ 的坐标；
3. （3）若曲线 $\text{[math]}$ 使得 $\text{[math]}$ 这些点分布在它的两侧，每侧各4个点，求出所有满足条件的整数 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2022九上·安徽开学考) 如图①，中国古代的马车已经涉及很复杂的机械设计（相对当时的生产力），包含大量零部件和工艺，所彰显的智慧让人拜服，如图②是马车的侧面示意图， $\text{[math]}$ 为车轮 $\text{[math]}$ 的直径，过圆心 $\text{[math]}$ 的车架 $\text{[math]}$ 一端点 $\text{[math]}$ 着地时，地面 $\text{[math]}$ 与车轮 $\text{[math]}$ 相切于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）徽徽猜想 $\text{[math]}$ ，徽徽的猜想正确吗？请说明理由；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ 米，求车轮的直径 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题

21. (2022九上·安徽开学考) 安徽省淮南市曹庵镇盛产草莓，有“中国草莓第一镇”之称，这里栽培草莓已有20多年的历史．曹庵草莓又好看又好吃，它长得如鸡心，红似玛瑙，果肉细腻多汁，而其苹果酸、柠檬酸、维生素，以及胡萝卜素、钙、磷、铁的含量也比苹果、梨、葡萄高 $\text{[math]}$ 倍，营养价值很高，被人们誉为“水果皇后”．果农老蜀种植了4亩草莓，恰逢市里有农产品大赛，老蜀计划从果农里随机摘下20枚草莓查看草莓的品质．

【收集数据】测得实际质量（单位： $\text{[math]}$ 如下：

42，41，21，36，30，30，31，36，33，38，32，32，30，36，41，35，32，31，31，32．

【整理数据】整理以上数据，得到如下不完整的每枚质量 $\text{[math]}$ 的频数分布表：

$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
1	3	$\text{[math]}$	4	3

【分析数据】根据以上数据，得到以下统计量：

统计量	平均数	中位数	方差
数据	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

根据以上信息，回答下列问题：

（1）表格中的 $\text{[math]}$ ， $\text{[math]}$ ；
（2）规定：若草莓的质量大于 $\text{[math]}$ 枚且不高于 $\text{[math]}$ 枚，则视为优品，此外都视为非优品．求本次采摘的优品率；
（3）已知优品比非优品每千克贵 $\text{[math]}$ 元，一次采摘的质量为 $\text{[math]}$ ，请估计这批货中的优品比相同质量的非优品可多卖多少元？

答案解析收藏纠错 + 选题

22. (2022九上·安徽开学考) 抛物线 $\text{[math]}$ 的对称轴为直线 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于 $\text{[math]}$ 和 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，将 $\text{[math]}$ 沿直线 $\text{[math]}$ 作对称，得到抛物线 $\text{[math]}$ ．
1. （1）求抛物线 $\text{[math]}$ 的解析式（写出自变量的取值范围）；
2. （2）直线 $\text{[math]}$ 与 $\text{[math]}$ 的另一个交点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别为线段 $\text{[math]}$ ， $\text{[math]}$ 上任意一点（不与 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 重合），作 $\text{[math]}$ 轴， $\text{[math]}$ 轴，分别交 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，设 $\text{[math]}$ 的最大值为 $\text{[math]}$ ， $\text{[math]}$ 的最大值为 $\text{[math]}$ ，求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
23. (2022九上·安徽开学考) 如图①，正方形 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 上一点， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 和 $\text{[math]}$ 的中点，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）求证： $\text{[math]}$ ；
3. （3）如图②，当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题