四川省成都市郫都区2023-2024学年高二上学期9月月考数...

更新时间：2023-10-17 浏览次数：43 类型：月考试卷

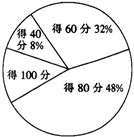
一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. (2023高二上·郫都月考) 已知 $\text{[math]}$ 是虚数单位，复数 $\text{[math]}$ 是纯虚数，则实数 $\text{[math]}$ 的值为（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . 4

答案解析收藏纠错 + 选题
2. (2023高二上·成都月考) 已知向量 $\text{[math]}$ 满足 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3 D . 4

答案解析收藏纠错 + 选题
3. (2023高二上·成都月考) 在 $\text{[math]}$ 中，若 $\text{[math]}$ ，则C等于（）

A . 45° B . 60°或120° C . 135° D . 45°或135°

答案解析收藏纠错 + 选题
4. (2023高二上·郫都月考) 某高中为了解学生课外知识的积累情况，随机抽取200名同学参加课外知识测试，测试共5道题，每答对一题得20分，答错得0分.已知每名同学至少能答对2道题，得分不少于60分记为及格，不少于80分记为优秀，测试成绩百分比分布图如图所示，则下列说法正确的是（）

A . 该次课外知识测试及格率为90% B . 该次课外知识测试得满分的同学有30名 C . 该次测试成绩的中位数大于测试成绩的平均数 D . 若该校共有3000名学生，则课外知识测试成绩能得优秀的同学大约有1440名

答案解析收藏纠错 + 选题
5. (2023高二上·郫都月考) 已知平面 $\text{[math]}$ ，直线 $\text{[math]}$ ，直线 $\text{[math]}$ 不在平面 $\text{[math]}$ 内，下列说法正确的是（）

A . 若 $\text{[math]}$ ，则 $\text{[math]}$ B . 若 $\text{[math]}$ ，则 $\text{[math]}$ C . 若 $\text{[math]}$ ，则 $\text{[math]}$ D . 若 $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023高二上·郫都月考) 将函数 $\text{[math]}$ 的图象向左平移 $\text{[math]}$ 个单位后，得到的函数图象关于 $\text{[math]}$ 轴对称，则 $\text{[math]}$ 的可能取值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023高二上·郫都月考) 在棱长为1的正方体 $\text{[math]}$ 中， $\text{[math]}$ 分别为 $\text{[math]}$ 的中点，过直线 $\text{[math]}$ 的平面 $\text{[math]}$ 平面 $\text{[math]}$ ，则平面 $\text{[math]}$ 截该正方体所得截面为（）

A . 三角形 B . 五边形 C . 平行四边形 D . 等腰梯形

答案解析收藏纠错 + 选题
8. (2023高二上·成都月考) $\text{[math]}$ 为 $\text{[math]}$ 所在平面内一点，且 $\text{[math]}$ ，则动点 $\text{[math]}$ 的轨迹必通过 $\text{[math]}$ 的（）

A . 垂心 B . 内心 C . 外心 D . 重心

答案解析收藏纠错 + 选题

二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分．

9. (2023高二上·郫都月考) 已知圆锥顶点为S，底面圆心为 $\text{[math]}$ 为底面的直径， $\text{[math]}$ 与底面所成的角为 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . 该圆锥的母线长为6 C . 该圆锥的体积为 $\text{[math]}$ D . 该圆锥的侧面积为 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023高二上·郫都月考) 已知 $\text{[math]}$ 的角 $\text{[math]}$ 所对的边分别为 $\text{[math]}$ 且 $\text{[math]}$ ，则下列说法正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 为等腰非等边三角形 D . $\text{[math]}$ 为等边三角形

答案解析收藏纠错 + 选题
11. (2023高二上·郫都月考) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， E为 $\text{[math]}$ 的中点， $\text{[math]}$ 与 $\text{[math]}$ 相交于 $\text{[math]}$ ，则下列说法一定正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ 在 $\text{[math]}$ 上的投影向量为 $\text{[math]}$ C . $\text{[math]}$ D . 若 $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2023高三上·渝北月考) 在正方体 $\text{[math]}$ 中， $\text{[math]}$ 是侧面 $\text{[math]}$ 上一动点，下列结论正确的是（）

A . 三棱锥 $\text{[math]}$ 的体积为定值 B . 若 $\text{[math]}$ ，则 $\text{[math]}$ 平面 $\text{[math]}$ C . 若 $\text{[math]}$ ，则 $\text{[math]}$ 与平面 $\text{[math]}$ 所成角为 $\text{[math]}$ D . 若 $\text{[math]}$ 平面 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 所成角的正弦最小值为 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本题共4小题，每小题5分，共20分． 

13. (2023高二上·成都月考) 用分层抽样的方法从某校高中学生中抽取一个容量为45的样本，其中高二年级有学生600人，抽取了15人．则该校高中学生总数是人．

答案解析收藏纠错 + 选题
14. (2023高二上·成都月考) 在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边上一点，且 $\text{[math]}$ ， P是 $\text{[math]}$ 上的一点，若 $\text{[math]}$ ，则实数 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
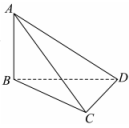
15. (2023高二上·成都月考) 在《九章算术》中，将四个面都是直角三角形的四面体称为鳖臑，在鳖臑 $\text{[math]}$ 中， $\text{[math]}$ 平面 $\text{[math]}$ ，已知动点 $\text{[math]}$ 从 $\text{[math]}$ 点出发，沿外表面经过棱 $\text{[math]}$ 上一点到点 $\text{[math]}$ 的最短距离为 $\text{[math]}$ ，则该棱锥的外接球的体积为．

答案解析收藏纠错 + 选题
16. (2023高二上·成都月考) 已知 $\text{[math]}$ 的内角 $\text{[math]}$ 的对边分别为 $\text{[math]}$ ，且 $\text{[math]}$ ，角 $\text{[math]}$ 的平分线与 $\text{[math]}$ 交于点 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题

四、解答题（本大题共6小题，共70分，17题10分，18-22题各12分，解答应写出文字说明、证明过程或演算步骤）

17. (2023高二上·郫都月考) 四棱锥 $\text{[math]}$ 的底面为正方形， $\text{[math]}$ 为 $\text{[math]}$ 的中点．
1. （1）证明： $\text{[math]}$ 平面 $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ 平面 $\text{[math]}$ ，证明： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2023高二上·成都月考) 设 $\text{[math]}$ 为平面内的四点，且 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，求 $\text{[math]}$ 点的坐标；
2. （2）设向量 $\text{[math]}$ ，若向量 $\text{[math]}$ 与 $\text{[math]}$ 平行，求实数 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
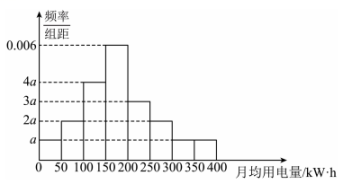
19. (2023高二上·郫都月考) 为了解某市家庭用电量的情况，统计部门随机调查了200户居民去年一年的月均用电量（单位： $\text{[math]}$ ），将全部数据按区间 $\text{[math]}$ 分成8组，得到如下的频率分布直方图：
1. （1）求图中a的值；并估计这200户居民月用电量的平均值（同一组中的数据用该组区间的中点值为代表）；
2. （2）为了既满足居民的基本用电需求，又提高能源的利用效率，市政府计划采用阶梯电价，使75%的居民缴费在第一档，20%的居民缴费在第二档，其余5%的居民缴费在第三档，试基于统计数据确定各档月均用电量的范围（计算百分位数时，结果四舍五入取整数）．
答案解析收藏纠错 + 选题
20. (2023高二上·郫都月考) 已知函数 $\text{[math]}$ 的图象如图所示
1. （1）求函数 $\text{[math]}$ 的解析式及单调递增区间；
2. （2）若函数 $\text{[math]}$ ，满足 $\text{[math]}$ 对任意的 $\text{[math]}$ 恒成立，求实数 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
21. (2023高二上·成都月考) 在 $\text{[math]}$ 中，角 $\text{[math]}$ 所对的边分别是 $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）求角 $\text{[math]}$ 的大小；
2. （2）若 $\text{[math]}$ 是锐角三角形，求 $\text{[math]}$ 的面积的取值范围．
答案解析收藏纠错 + 选题
22. (2023高二上·成都月考) 如图， $\text{[math]}$ 是平面四边形， $\text{[math]}$ 为正三角形， $\text{[math]}$ ．将 $\text{[math]}$ 沿 $\text{[math]}$ 翻折，过点 $\text{[math]}$ 作平面 $\text{[math]}$ 的垂线，垂足为 $\text{[math]}$ ．
1. （1）若点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，求 $\text{[math]}$ 的长；
2. （2）若点 $\text{[math]}$ 在 $\text{[math]}$ 内部，且直线 $\text{[math]}$ 与平面 $\text{[math]}$ 所成角的正弦值为 $\text{[math]}$ ，求二面角 $\text{[math]}$ 的余弦值．
答案解析收藏纠错 + 选题