陕西省汉中市西乡县2023-2024学年高二上册数学开学考试...

更新时间：2023-10-09 浏览次数：34 类型：开学考试

一、选择题：本大题共8小题，每小题5分，共计40分，每小题给出的四个选项中，只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.

1. (2023高二上·西乡县开学考) 下列与 $\text{[math]}$ 角的终边相同的角的表达式中，正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023高二上·西乡县开学考) $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023高二上·西乡县开学考) 函数 $\text{[math]}$ 的定义域是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023高二上·西乡县开学考) 若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024高一下·南宁期末) 如图，在正方体 $\text{[math]}$ 中，异面直线 $\text{[math]}$ 与 $\text{[math]}$ 所成的角为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023高二上·西乡县开学考) 已知角 $\text{[math]}$ 是第一象限角， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023高二上·西乡县开学考) 已知向量 $\text{[math]}$ 、 $\text{[math]}$ 满足 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则一定共线的三点是（）

A . A ， B ， D B . A ， B ， C C . B ， C ， D D . A ， C ， D

答案解析收藏纠错 + 选题
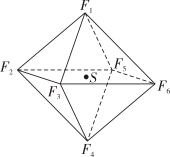
8. (2023高二上·西乡县开学考) 六氟化硫，化学式为 $\text{[math]}$ ，在常压下是一种无色、无毒、不燃的稳定气体，有良好的绝缘性，在电器工业方面具有广泛用途．如图所示，其分子结构是六个氟原子处于顶点位置，而硫原子处于中心位置的正八面体，也可将其六个顶点看作正方体各个面的中心点．若正八面体的表面积为 $\text{[math]}$ ，则正八面体外接球的体积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、选择题：本大题共4小题，每小题5分，共计20分，每小题给出的四个选项中，有多项符合题目要求.全部选对得5分，选对但不全得2分，有选错得得0分.

9. (2023高二上·西乡县开学考) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是平面内三个非零向量，则下列结论正确的是（）

A . 若 $\text{[math]}$ ，则 $\text{[math]}$ B . 若 $\text{[math]}$ ，则 $\text{[math]}$ C . 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ D . 若 $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023高二上·西乡县开学考) 在 $\text{[math]}$ 中，角A ， B ， C所对的边为a ， b ， c ，则下列说法正确的有（）

A . A：B：C=a：b：c B . $\text{[math]}$ C . 若A>B ，则a>b D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2023高二上·西乡县开学考) 设函数 $\text{[math]}$ ，则下列结论正确的有（）

A . $\text{[math]}$ 的最小正周期为 $\text{[math]}$ B . $\text{[math]}$ 在区间 $\text{[math]}$ 上单调递减 C . $\text{[math]}$ 的图象关于点 $\text{[math]}$ 对称 D . $\text{[math]}$ 的图象关于直线 $\text{[math]}$ 对称

答案解析收藏纠错 + 选题
12. (2023高二上·西乡县开学考) 如图，以等腰直角三角形斜边 $\text{[math]}$ 上的高 $\text{[math]}$ 为折痕，把 $\text{[math]}$ 和 $\text{[math]}$ 折成互相垂直的两个平面后，则下列四个结论中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ 是等边三角形 C . 平面 $\text{[math]}$ 平面 $\text{[math]}$ D . 二面角 $\text{[math]}$ 的正切值为 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本大题共4小题，每小题5分，共计20分.

13. (2023高二上·西乡县开学考) 已知平面向量 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 的夹角为 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2023高二上·西乡县开学考) 已知 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2023高二上·西乡县开学考) 如图，四边形 $\text{[math]}$ 是梯形 $\text{[math]}$ 的直观图，四边形 $\text{[math]}$ 是等腰梯形，且 $\text{[math]}$ ，则梯形 $\text{[math]}$ 的周长为.

答案解析收藏纠错 + 选题
16. (2023高二上·西乡县开学考) 已知一个球与一个正三棱柱 $\text{[math]}$ 的三个侧面和两个底面都相切，且这个球的体积为 $\text{[math]}$ ，那么这个三棱柱的侧面积为，二面角 $\text{[math]}$ 的正弦值为．

答案解析收藏纠错 + 选题

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

17. (2023高二上·西乡县开学考) 已知i是虚数单位， $\text{[math]}$ .
1. （1）求 $\text{[math]}$ ；
2. （2）若复数 $\text{[math]}$ 的虚部为-1，且 $\text{[math]}$ 是纯虚数，求 $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2023高二上·西乡县开学考) 已知函数 $\text{[math]}$ (其中 $\text{[math]}$ ， $\text{[math]}$ )的图象如图所示.
1. （1）求函数 $\text{[math]}$ 的解析式；
2. （2）若将函数 $\text{[math]}$ 的图象上的所有点的纵坐标不变，横坐标伸长到原来的3倍，得到函数 $\text{[math]}$ 的图象，求当 $\text{[math]}$ 时，函数 $\text{[math]}$ 的单调递增区间.
答案解析收藏纠错 + 选题
19. (2023高二上·西乡县开学考) 已知平面向量 $\text{[math]}$ ， $\text{[math]}$ ，函数 $\text{[math]}$ .
1. （1）求函数 $\text{[math]}$ 相邻两对称轴的距离；
2. （2）求函数 $\text{[math]}$ 在区间 $\text{[math]}$ 上的值域.
答案解析收藏纠错 + 选题
20. (2023高二上·西乡县开学考) 如图，在正三棱柱 $\text{[math]}$ （侧棱垂直于底面，且底面是正三角形）中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中点.
1. （1）求证：平面 $\text{[math]}$ 平面 $\text{[math]}$ ；
2. （2）求证： $\text{[math]}$ 平面 $\text{[math]}$
答案解析收藏纠错 + 选题
21. (2023高二上·西乡县开学考) 在锐角 $\text{[math]}$ 中， $\text{[math]}$ 的对边分别为 $\text{[math]}$ ，且 $\text{[math]}$
1. （1）确定角 $\text{[math]}$ 的大小；
2. （2）若 $\text{[math]}$ ，且 $\text{[math]}$ ，求边 $\text{[math]}$ .
答案解析收藏纠错 + 选题
22. (2023高二上·西乡县开学考) 如图，在三棱柱 $\text{[math]}$ 中， $\text{[math]}$ 底面 $\text{[math]}$ ，且 $\text{[math]}$ 为等边三角形， $\text{[math]}$ ，D为 $\text{[math]}$ 的中点．
1. （1）求证：直线 $\text{[math]}$ 平面 $\text{[math]}$ ；
2. （2）求证：平面 $\text{[math]}$ 平面 $\text{[math]}$ ；
3. （3）求三棱锥 $\text{[math]}$ 的体积．
答案解析收藏纠错 + 选题