广东省深圳市罗湖区2022-2023学年多校联考八年级上册数...

更新时间：2023-10-24 浏览次数：31 类型：开学考试

一、选择题（本题共有12小题，每小题3分，共36分，每小题有四个选项，其中有一个是正确的）

1. (2022八上·罗湖开学考) 化简x⁶÷x²的结果是（）

A . x⁸ B . x⁴ C . x³ D . x

答案解析收藏纠错 + 选题
2. (2022八上·罗湖开学考) 下面有4个汽车标志图案，其中是轴对称图形的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
3. (2022八上·罗湖开学考) 下列说法正确的是（）

A . 如果两个三角形的周长相等，那么这两个三角形一定全等 B . 同位角相等 C . 在同一平面内经过直线外一点有且只有一条直线与已知直线平行 D . 一个角的补角一定是钝角

答案解析收藏纠错 + 选题
4. (2022八上·罗湖开学考) 我国雾霾天气多发，PM_2.5颗粒物被称为大气的元凶．PM_2.5是指直径小于或等于2.5微米的颗粒物，已知1毫米＝1000微米，用科学记数法表示2.5微米（）

A . 2.5×10³毫米 B . 2.5×10^-3毫米 C . 0.25×10^-2毫米 D . 2.5×10^-4毫米

答案解析收藏纠错 + 选题
5. (2022八上·罗湖开学考) 用直尺和圆规作一个角等于已知角，如图，能得出∠A'O'B'＝∠AOB的依据是（）

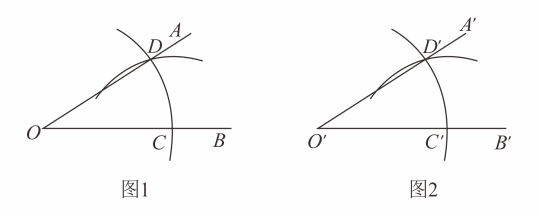
A . SAS B . ASA C . AAS D . SSS

答案解析收藏纠错 + 选题
6. (2022八上·罗湖开学考) 如图，将一块三角尺的直角顶点放在直线a上，a∥b ，则∠2＝（）

A . 80° B . 70° C . 60° D . 50°

答案解析收藏纠错 + 选题
7. (2022八上·罗湖开学考) 下列事件是必然事件的是（）

A . 购买一张体育彩票，中奖 B . 任意掷一枚色子，其点数为奇数 C . 打开电视机，任选一个频道，屏幕上正在播放新闻联播 D . 任意画一个三角形，其内角和是180°

答案解析收藏纠错 + 选题
8. (2022八上·罗湖开学考) 当n＝（）时，x²+2（n-3）x+16是完全平方式．

A . 7 B . 1或-1 C . -1或7 D . -1

答案解析收藏纠错 + 选题
9. (2022八上·罗湖开学考) 一支签字笔的单价为2.5元，小涵同学拿了100元钱去购买了x（x≤40）支该型号的签字笔，写出所剩余的钱y与x间的关系式（）

A . y＝2.5x B . y＝100-2.5x C . y＝2.5x-100 D . y＝100+2.5x

答案解析收藏纠错 + 选题
10. (2022八上·罗湖开学考) 如图，OP平分∠MON ， PA⊥ON于点A ，若PA＝2，则PQ最小值为（）

A . 3 B . 2 C . 1 D . 1.5

答案解析收藏纠错 + 选题
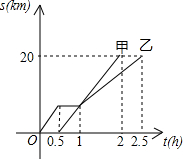
11. (2022八上·罗湖开学考) 甲、乙两同学骑自行车从A地沿同一条路到B地，已知如图，甲做匀速运动，他们离出发地距离s（km）和骑车行驶时间t（h），给出下列说法：
①他们都骑车行驶了20km；

②乙在途中停留了0.5h；

③甲、乙两人同时到达目的地；

④相遇后，甲的速度小于乙的速度．

根据图象信息，以上说法错误的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
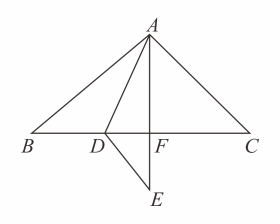
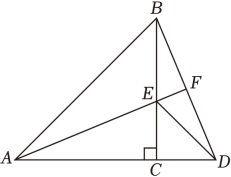
12. (2022八上·罗湖开学考) 如图，已知△ABC与△CDE均为等腰直角三角形，点E在BC边上，连接BD，AE的延长线交BD于点F ，且AE平分∠BAC ，则下列结论中：①△ACE≌△BCD；②AF⊥BD；③AE＝2DF；④EF平分∠BED.正确的个数是（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题（每小题3分，共12分）请把答案填在答题卷相应的位置．

13. (2022八上·罗湖开学考) 一个不透明的布袋里装有8个只有颜色不同的球，其中5个红球、3个白球，从布袋中随机摸出一个球，则摸到红球的概率是．

答案解析收藏纠错 + 选题
14. (2022八上·罗湖开学考) 计算（mn）³的结果是．

答案解析收藏纠错 + 选题
15. (2022八上·罗湖开学考) 如图，矩形的长、宽分别为a、b ，（a＞b）周长为20，面积为16，则a-b的值为．

答案解析收藏纠错 + 选题
16. (2022八上·罗湖开学考) 如图，C为线段AE上一动点（不与A，E重合），在AE同侧分别作等边△ABC和等边△ECD，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，则有以下五个结论：①AD＝BE；②PQ∥AE；③△PCQ为轴对称图形；④DP＝DE；⑤∠AOB＝60°．以上结论正确的是（填序号）.

答案解析收藏纠错 + 选题

三、解答题：第17题8分，第18，19每题6分，第20题8分，第21题7分，第22题8分，第23题9分，共52分．

17. (2022八上·罗湖开学考) 计算：
1. （1）（- $\text{[math]}$ ）^-2×（-2）⁰+|-5|×（-1）³；
2. （2）（m+2n）（m-2n）-4n（m-n）．
答案解析收藏纠错 + 选题
18. (2022八上·罗湖开学考) 先化简，再求值：[（a+2b）²-（3a+b）（3a-b）-5b²]÷（2a），其中a＝- $\text{[math]}$ ， b＝-1．

答案解析收藏纠错 + 选题
19. (2022八上·罗湖开学考) 现有两个大的盒子，甲盒里装有红球5个，白球2个和黑球13个，乙盒里装有红球20个，白球20个和黑球10个．
1. （1）如果你随机取出1个黑球，选哪个盒子成功的机会大？请说明理由．
2. （2）小明同学说“从乙盒取出10个红球后，乙盒中的红球个数仍比甲袋中红球个数多，所以此时想取出1个红球，选乙盒成功的机会大.“你认为此说法正确吗?为什么？”（要从概率的角度说明，否则不得分）
答案解析收藏纠错 + 选题
20. (2022八上·罗湖开学考) 填空：把下面的推理过程补充完整，并在括号内注明理由．
已知：如图，△ABC中，D、E分别为AB、AC的中点，过点C作CF∥AB交DE的延长线于F，求证：AB＝2CF ．

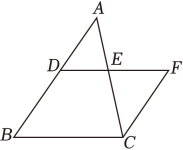
证明：∵CF∥AB（           ），

∴∠ADE＝∠F（           ），

∵E为AC的中点（已知），

∴AE＝CE（          ），

在△ADE与△CFE中，

∠ADE＝∠F ，           ＝          ， AE＝CD ，

∴△ADE≌△CFE（          ），

∴AD＝CF（           ），

∵D为AB的中点，

∴AB＝2AD（中点的定义），

∴AB＝2CF（           ）．

答案解析收藏纠错 + 选题
21. (2022八上·罗湖开学考) 如图，方格纸中的每个小方格都是边长为1个单位的正方形，△ABC的顶点均在格点上，直线a为对称轴，点A ，点C在直线a上．
1. （1）作△ABC关于直线a的轴对称图形△ADC；
2. （2）若∠BAC＝35°，则∠BDA＝；
3. （3） △ABD的面积等于．
答案解析收藏纠错 + 选题
22. (2022八上·罗湖开学考) 如图，已知△ABC中，∠B＝∠E＝40°，且AD平分∠BAE ．
1. （1）求证：BD＝DE；
2. （2）若AB＝CD ，求∠ACD的大小．
答案解析收藏纠错 + 选题
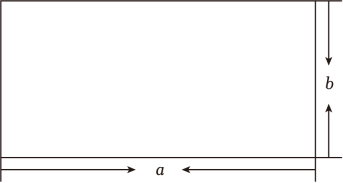
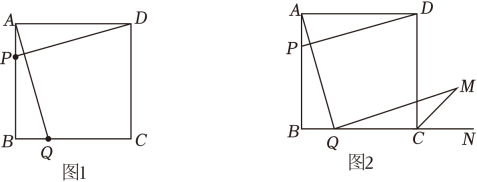
23. (2022八上·罗湖开学考) 漂洋同学在暑假自学探究过程中发现有一种特殊的四边形，它的四边都相等，且四个角都是直角，我们把具有这种性质的四边形叫做正方形，请你利用上面的信息解答下列问题：如图1，在正方形ABCD中，边长AB＝8cm ，点P以2cm/s的速度自点A向终点B运动，点Q同时以同样的速度自点B向终点C运动，连接AQ、DP，设运动时间为ts.
1. （1）当t＝s时，点P到达点B；
2. （2）在点P、Q运动过程中，试判断AQ、DP有什么样的位置和数量关系；
3. （3）如图2，作QM⊥AQ ，作∠DCN的角平分线交QM于M点，AQ与QM的数量关系是否发生改变，若不改变请说明理由．
答案解析收藏纠错 + 选题