一、选择题(本大题共14个小题,共38分,1~10小题每小题3分,11~14小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)
-
-
-
-
-
A . 等角的补角相等
B . 如果两个角相等,那么它们的余角也相等
C . 如果两个角的余角相等,那么这两个角相等
D . 同角的余角相等
-
6.
(2023八上·襄都月考)
对于代数式

有甲、乙两种判断,其中正确的是( )
甲:是分式,因为 是整式,且分母
是整式,且分母 中含有字母;
中含有字母;
乙:是整式,因此 , 而1是整式;
, 而1是整式;
A . 甲对
B . 乙对
C . 甲和乙均对
D . 甲和乙均不对
-
-
-
-
-
A . x
B .  C . 3
D .
C . 3
D . 
-
12.
(2023八上·襄都月考)
如图,把一长一短两根细木棍的一端用螺钉铰合在一起,使长木棍的另一端与射线
BC的端点
B重合,固定住长木棍,摆动短木棍,使端点分别落在射线
BC上的
C、
D两位置时,形成了

和

. 此时

, 但是

和

不全等,这说明( )

A . 三角对应相等的两个三角形不一定全等
B . 两边及一边对角对应相等的两个三角形不一定全等
C . 两角及一角对边对应相等的两个三角形不一定全等
D . 两边及夹角对应相等的两个三角形不一定全等
-
13.
(2023八上·襄都月考)
老师设计了接力游戏,甲、乙、丙、丁四位同学用合作的方式完成分式化简.规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,整个化简过程如图所示,接力中,自己负责的一步出现错误的同学是( )

A . 甲和乙
B . 乙和丙
C . 丙和丁
D . 甲和丁
-
14.
(2023八上·襄都月考)
某学校为进一步开展“阳光大课间”活动,购买了一批篮球和足球.已知购买足球数量是篮球的2倍,购买足球用了4000元,购买篮球用了2800元,篮球的单价比足球贵16元.篮球和足球的单价分别是多少元?小明列出了方程

, 则小明列的方程中
x表示的是( )
A . 足球的单价
B . 篮球的单价
C . 足球的数量
D . 篮球的数量
二、填空题(本大题共3个小题,共10分.15小题2分,16~17小题各4分,每空2分)
-
-
16.
(2023八上·襄都月考)
小玉要打一份40000字的文件,第一天她打字1.5小时,打字速度为
a字/分.第二天她打字速度比第一天快了20字/分,两天打完全部文件,请用含
a的式子表示
⑴第一天打字的个数为;
⑵第二天打字用的时间为分.
-
17.
(2023八上·襄都月考)
如图,
AE与
BD相交于点
C ,

, 点
P从点
A出发,沿
A→
B→
A方向以

的速度运动,点
Q从点
D出发,沿
D→
E方向以

的速度运动,
P、
Q两点同时出发,当点
P到达点
A时,
P、
Q两点同时停止运动,设点
P的运动时间为
t(
s).用含
t的式子表示


;连接
PQ , 若线段
PQ经过点
C时,则
 s
s .

三、解答题(本大题共七题,满分72分,解答题应写出必要的解题步骤或文字说明)
-
-
19.
(2023八上·襄都月考)
命题:在同一平面内,垂直于同一条直线的两条直线互相平行、如下给出了不完整的“已知”和“求证”,请补充完整,并写出证明过程(注明理由).

已知:如图, , ▲ .
, ▲ .
求证: ▲ .
-
-
-
(2)
小华说“我看到答案是原分式方程的解为

”,请你求出原分式方程中“▲”代表的数.
-
21.
(2023八上·襄都月考)
为了测量楼
AB的高度,在旗杆
CD与楼
AB之间选定一点
P , 测得旗杆顶端
C的视线
PC与水平线的夹角

, 楼顶
A的视线
PA与水平线的夹角

, 点
P到楼底的距离
BP与旗杆
CD的高度均为

, 旗杆
CD与楼
AB之间的距离
DB为

, 求楼
AB的高度.

-
22.
(2023八上·襄都月考)
老师布置了今天的作业:用两种方法计算

.
下面是嘉淇同学作业中的部分运算过程:
解:原式 第一步
第一步
 第二步
第二步
 第三步
第三步
 第四步
第四步
 ……
……
-
-
-
23.
(2023八上·襄都月考)
园林小队进行一段江岸的绿化,在合同期内高效地完成了任务,这是记者与该队工程师的一段对话:

记者 | 你们是怎样提前3小时完成了180平方米的绿化任务? |

工程师 | 我们的施工人数由原计划的6人,增加了2人. |
如果每人每小时的绿化面积相同,求每人每小时的绿化面积.
-
-
(1)
已知

, 则

.
-
(2)
求五边形
ABCDE的周长.
【注:五边形的周长指组成五边形的所有边的和】
 B .
B .  C .
C . 
 B .
B . 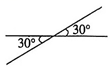 C .
C . 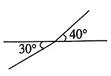 D .
D . 




, ▲ .
