![]()
![]()


![]()
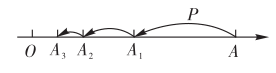
①在小猫未抓住老鼠前,用时间t(秒)的代数式表示老鼠和小猫在移动过程中分别与点A之间的距离;
②小猫逮住老鼠时的“位置”恰好在 , 求时间t.
知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
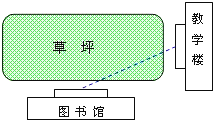
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.
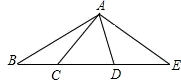
情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
数轴上表示和
的两点之间的距离是
, 而
;表示
和
两点之间的距离是
, 而
;表示
和
两点之间的距离是
, 而
.
一般地,数轴上表示数和数
的两点之间的距离公式为
.
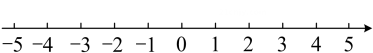
①问为何值时,
为
的中点?
②当时,求
的值.

![]()