一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
-
-
A . 若 , 则
, 则 B . 若
B . 若 , 则
, 则 C . 若
C . 若 , 则
, 则 D . 若
D . 若 , 则
, 则
-
-
-
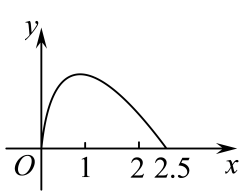
6.
(2023高一上·温州期中)
如图,点
P在边长为1的正方形边上运动,
M是
CD的中点,当点
P沿

运动时,点
P经过的路程
x与

的面积
y的函数

的图象的形状大致是( )

-
-
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对得5分,部分选对得2分,有选错的得0分.
-
A . 函数 在
在 上单调递增,在
上单调递增,在 上单调递增,则
上单调递增,则 在
在 上是增函数
B . 函数
上是增函数
B . 函数 的零点是
的零点是 、
、 C . 设
C . 设 、
、 , 则“
, 则“ ,
,  ”是“
”是“ ”充分不必要条件
D .
”充分不必要条件
D .  和
和 表示同一个函数
表示同一个函数
-
A . 若 , 则
, 则 B . 若
B . 若 , 则
, 则 C . 若
C . 若 , 则
, 则 D . 若
D . 若 , 则
, 则
-
A .  有最小值
有最小值 B .
B .  有最小值
有最小值 C . 函数
C . 函数 的最小值为1
D .
的最小值为1
D .  有最大位
有最大位
-
A . 函数 的最大值可能是
的最大值可能是 B . 函数
B . 函数 的图象一定具有对称性
C . “函数
的图象一定具有对称性
C . “函数 最大值为1”是“
最大值为1”是“ ,
,  ”的必要不充分条件
D . 函数
”的必要不充分条件
D . 函数 在定义域内不可能是单调函数
在定义域内不可能是单调函数
三、填空题:本题共4小题,每小题5分,共20分.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或验算步骤.
-
-
-
(1)
求

和

;
-
(2)
若集合

(
a为常数),且

, 求实数
a的取值范围.
-
-
(1)
若

为奇函数,求实数
a的值;
-
(2)
在(1)的条件下,试判断

在

上的单调性并用定义法给出证明,写出此时

的值域.
-
20.
(2023高一上·温州期中)
杭州第19届亚运会,温州分会场场馆之一的温州体育中心,内有一块足够长的矩形场地,一面靠墙,现需要分隔出志愿者区、记者区以及运动员候场区三块区域如图,除墙外的各边界线用安全警戒带围成.现有40m长的安全警戒带材料.

-
(1)
若运动员候场区面积是志愿者区与记者区面积之和,运动员候场区长、宽分别设计为多少时,可使其面积最大,最大面积是多少平米?
-
(2)
在保证志愿者区和记者区面积之和是20平米的前提下,如何设计运动员候场区的长、宽,可以使得运动员候场区的面积最大?
-
-
(1)
试判断函数

的奇偶性,并给出证明;
-
(2)
设函数

, 请判断

在

上的单调性,并求不等式

的解.
-
-
(1)
当

时,求

在区间

上的最大值(用含
b的式子表示);
-
(2)
如果方程

有三个不相等的实数解

,

,

, 求

的取值范围.
 B .
B .  C .
C .  D .
D . 
 B .
B . 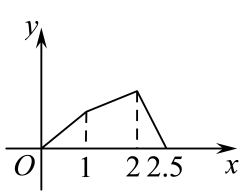 C .
C .  D .
D .