 B .
B .  C .
C .  D .
D . 


 B .
B . 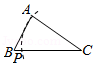 C .
C . 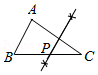 D .
D . 

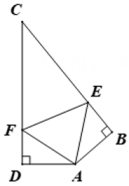



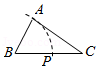
(1)作出三角形ABC的角平分线CD;
(2)作出三角形ABC的中线BE.

问题:如图,在△ABC中,∠ABC=∠ACB,点D在AB边上(不与点A、点B重合),点E在AC边上(不与点A、点C重合),连接BE、CD,BE与CD相交于点F.若 ▲ , 求证:BE=CD.

逆命题: ▲ .
已知:AB是一条线段,P是一点,且 ▲ ;求证: ▲ .
证明:(1)当P在线段AB上时,结论显然成立;
当点P不在线段AB上时,如图(请继续完成证明过程)


如图1,若点D在边BA的延长线上,求证:AD+BC=BE;
如图2,若点D在线段AB上,请直接写出线段AD、BC与BE之间存在怎样的数量关系;
如图3若点D在线段AB的延长线上,请探究线段AD、BC与BE之间的数量关系,并证明.
