一、选择题:以下每小题均有A,B,C,D四个选项,其中只有一个选项正确,每小题3分,共36分.
-
A . 从江县明天将有30%的地区降水
B . 从江县明天将有30%的时间降水
C . 从江县明天降水的可能性较小
D . 从江县明天肯定不降水
-
2.
(2023九上·从江期中)
李老师为帮助学生正确理解物理变化与化学变化,将6种生活现象分别写在6张卡片上(如图所示),卡片的背面完全相同,将卡片正面朝下洗匀后.从中随机抽取一张卡片,抽中生活现象是物理变化的概率是( )

-
3.
(2024九上·西湖期末)
某班级计划举办手抄报展览,确定了“5G时代”、“北斗卫星”、“高铁速度”三个主题,若小明和小亮每人随机选择其中一个主题,则他们恰好选择同一个主题的概率是( )
-
4.
(2023九上·从江期中)
小明的不透明袋中有除颜色外都相同的红、黄、蓝、白球若干个,晓晓又放入5个黑球,通过多次摸球试验,发现摸到红球、黄球、蓝球、白球的频率依次为30%,15%,40%,10%,则小明的袋中黄球大约有( )
A . 5个
B . 10个
C . 15个
D . 30个
-
5.
(2023九上·从江期中)
如图所示的是两个可以自由转动的均匀转盘A和B,转盘A,B分别被均匀地分成三等份和四等份,同时自由转动转盘A和B,转盘停止后,指针各指向一个数字(如果指针恰好在分格线上,那么重转一次,直至指针指向某一数字为止),则两个数字的积为偶数的概率是( )

-
6.
(2023九上·从江期中)
有三张正面分别写有数字-2,1,3的卡片,它们背面完全相同,现将这三张卡片背面朝上洗匀后随机抽取一张,以其正面数字作为a的值,然后把这张放回去,洗匀后,再从三张卡片中随机抽一张,以其正面的数字作为b的值,则点(a,b)在第一象限的概率为( )
-
7.
(2023九上·从江期中)
某展览大厅有2个入口和2个出口,其示意图如图所示,参观者可从任意一个入口进入,参观结束后可从任意一个出口离开,则一位参观者从入口1进入并从出口A离开的概率是( )

-
8.
(2023九上·从江期中)
绿豆在相同条件下的发芽试验,结果如表所示:
每批 粒数n | 100 | 300 | 400 | 600 | 1 000 | 2 000 | 3 000 |
发芽的 粒数m | 96 | 282 | 382 | 570 | 948 | 1 904 | 2 850 |
发芽的 频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
下面有三个推断:
①当n=400时,绿豆发芽的频率为0.955,所以绿豆发芽的概率是0.955;
②根据上表,估计绿豆发芽的概率是0.95;
③若n为4 000,估计绿豆发芽的粒数为 3 800 粒.
其中推断合理的是( )
A . ①
B . ①②
C . ①③
D . ②③
-
9.
(2023九上·从江期中)
在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.若随机摸出一个小球后不放回,再随机摸出一个小球,则两次取出小球标号的和等于5的概率为( )
-
10.
(2023九上·从江期中)
班长邀请A,B,C,D四位同学参加圆桌会议.如图所示,班长坐在⑤号座位,四位同学随机坐在①②③④四个座位,则A,B两位同学座位相邻的概率是( )

-
-
12.
(2023九上·从江期中)
如图所示,有一边长为6 cm的等边三角形ABC木块,点P是CA的延长线上的点,AP为15 cm,其中

,

,

的圆心依次为A,B,C,则曲线PDFE的长是( )

A . 18π cm
B . 15π cm
C . 20π cm
D . 21π cm
二、填空题:每小题4分,共16分.
-
13.
(2023九上·从江期中)
九年级(1)班的教室里正在召开50人的座谈会,其中有8名教师,12名家长,30名学生,当校长走到教室门口时,听到里面有人在发言,那么发言人是家长的概率为
.
-
14.
(2023九上·从江期中)
某林业部门统计某种幼树在一定条件下的移植成活率,结果如表所示:
移植总 数(n) | 400 | 750 | 1 500 | 3 500 | 7 000 | 9 000 | 14 000 |
成活数 (m) | 369 | 662 | 1 335 | 3 203 | 6 335 | 8 073 | 12 628 |
成活的 频率 | 0.923 | 0.883 | 0.890 | 0.915 | 0.905 | 0.897 | 0.902 |
根据表中数据,估计这种幼树移植成活的概率为(精确到0.1).
-
15.
(2023九上·从江期中)
如图所示,在Rt△AOB中,OA=OB=4

, ☉O的半径为2,点P是AB边上的动点,过点P作☉O的一条切线PQ(点Q为切点),则线段PQ长的最小值为
.

-
16.
(2023九上·从江期中)
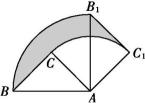
如图所示,在△ABC中,∠ACB=90°,AC=BC=2.将△ABC绕着点A顺时针旋转90度到△AB
1C
1的位置,则边BC扫过区域(阴影部分)的面积为
(结果用含π的式子表示).
三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.
-
17.
(2023九上·从江期中)
一只不透明的袋子中装有3个大小、质地完全相同的乒乓球,球面上分别标有数字1、2、3,搅匀后先从袋子中任意摸出1个球,记下数字后放回,搅匀后再从袋子中任意摸出1个球,记下数字.
-
-
(2)
用画树状图或列表等方法求两次都摸到标有奇数的乒乓球的概率.
-
18.
(2023九上·从江期中)
如图所示,数轴上的点A,B,C,D表示的数分别为-3,-1,1,2,从A,B,C,D四点中任意取两点,求所取两点之间的距离为2的概率.

-
-
20.
(2023九上·从江期中)
如图所示有两个可以自由转动的转盘A,B,小明与小李用它们做配紫色(红色与蓝色配成紫色)游戏:让两个转盘分别自由转动一次,当两个转盘停止时,如指针所指区域的颜色分别是一红一蓝,就说“配成紫色”,小明胜;如果指针所指区域的颜色配不成紫色,则小李胜.
-
(1)
利用画树状图或列表等方法表示游戏所有可能出现的结果.
-
(2)
这个游戏对双方公平吗?请说明理由.

-
21.
(2023九上·从江期中)
已知一只纸箱中装有除颜色外完全相同的红色、黄色、蓝色乒乓球共100个.从纸箱中任意摸出一球,记下颜色后放回,多次试验后,测得:摸到红色乒乓球、黄色乒乓球的频率分别稳定在20%和30%左右.
-
-
(2)
假设向纸箱中再放进红色乒乓球x个,这时从纸箱中任意取出一个球是红色乒乓球的概率为0.5,试求x的值.
-
22.
(2023九上·从江期中)
如图所示,PA,PB是☉O的切线,CD切☉O于点E,△PCD的周长为12,∠APB=60°.求:

-
-
-
23.
(2023九上·从江期中)
在阳光体育活动时间,小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一张空球桌,他们只能选两人打第一场.
-
(1)
如果确定小亮打第一场,再从其余三人中随机选取一人打第一场,求恰好选中大刚的概率.
-
(2)
如果确定小亮做裁判,用“手心、手背”的方法决定其余三人哪两人打第一场.游戏规则是:三人同时伸“手心、手背”中的一种手势,如果恰好有两人伸出的手势相同,那么这两人上场,否则重新开始,这三人伸出“手心”或“手背”都是随机的,请用画树状图的方法求小莹和小芳打第一场的概率.
-
24.
(2023九上·从江期中)
如图⑴所示的是一枚质地均匀的正四面体形状的骰子,每个面上分别标有数字1,2,3,4,如图⑵所示是一个正六边形棋盘,现通过掷骰子的方式玩跳棋游戏,规则是将这枚骰子掷出后,看骰子向上三个面(除底面外)的数字之和是几,就从图⑵中的A点开始沿着顺时针方向连续跳动几个顶点,第二次从第一次的终点处开始,按第一次的方法跳动.
-
(1)
随机掷一次骰子,则棋子跳动到点C处的概率是;
-
(2)
随机掷两次骰子,用画树状图或列表的方法,求棋子最终跳动到点C处的概率.

-
25.
(2023九上·从江期中)
“垃圾分类”越来越受到人们的关注,我市某中学对部分学生就垃圾分类知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:

-
(1)
接受问卷调查的学生共有人,条形统计图中m的值为;
-
(2)
扇形统计图中“了解很少”部分所对应扇形的圆心角的大小为;
-
(3)
若该中学共有学生1800人,根据上述调查结果,可以估计出该学校学生中对垃圾分类知识达到“非常了解”和“基本了解”程度的总人数为;
-
(4)
若从对垃圾分类知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加垃圾分类知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.





![]()



