一、选择题(本大题共12个小题,每小题3分,共36分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)
-
-
A . 5个
B . 4个
C . 3个
D . 2个
-
-
A . (x-2)2=7
B . (x+2)2=1
C . (x-2)2=1
D . (x+2)2=2
-
-
-
7.
(2023九上·威远期中)
如图,某小区计划在一个长

米,宽

米的矩形场地

上修建三条同样宽的道路,使其中两条与

平行,另一条与

平行,其余部分种草.若使每块草坪面积都为

平方米,设道路的宽度为

米,则可列方程为( )

-
-
A . 12
B . 13
C . 14
D . 15
-
10.
已知一元二次方程

的两个根为

、

, 则

的值为( )
A . -3
B .  C . 1
D .
C . 1
D . 
-
-
12.
(2023九上·威远期中)
如图,把菱形

向平移至

的位置,作

, 垂足为

与

相交于点

的延长线交

于点

, 连接

, 则下列结论:①

;②

;③

;④

, 则正确的结论有( )个
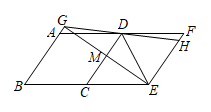
A . 1
B . 2
C . 3
D . 4
二、填空题(本大题共4个小题,每小题5分,共20分,答案写在答题卡上)
-
-
-
-
16.
(2023九上·威远期中)
如图,小明在

测得某树的影长为

,

时又测得该树的影长为

, 若两次日照的光线互相垂直,则这棵树的高度为
.

三、解答题
-
-
(1)

;
-
(2)

.
-
-
(1)

-
(2)

-
19.
(2023九上·威远期中)
某地由于台风受灾牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款

元,第三天收到捐款

元.
-
(1)
如果第二天、第三天收到捐款的增长率相同,求捐款增长率;
-
(2)
按照(1)中收到捐款的增长率不变,求该单位这三天共收到捐款多少元?
-
-
(1)
求证:

;
-
-
21.
(2023九上·威远期中)
如果关于x的一元二次方程

有两个实数根,且其中一个根是另一个根的3倍,那么称这样的方程为“三倍根方程”.例如,方程

的两个根是1和3,则这个方程就是“三倍根方程”.
-
-
(2)
若关于n的方程

是“三倍根方程”,则

;(写出必要步骤)
-
(3)
若

是关于x的“三倍根方程”,求代数式

的值.
四、填空题(本大题共4个小题,每小题6分,共24分,答案写在答题卡上)
-
-
-
-
25.
(2023九上·威远期中)
如图,点A是反比例函数

图象上的一点,过A作

轴于点B,点D为x轴正半轴上一点且

, 连接

交y轴于点C,连接

. 若

的面积为4,则k的值为
.

五、解答题(本小题共3个小题,每小题12分,共36分,答案写在答题卡上)
-
26.
(2023九上·威远期中)
随着气温的降低,乌市某电器商场销售一批电暖器,平均每天可售出30台,每台可盈利50元,为了扩大销售量,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每台每降价1元,商场平均每天可多售出2台.设每台降价

元,则:
-
(1)
每天可销售
台,每台盈利
元(用含

的式子表示)
-
(2)
在尽快减少库存的前提下,商场每天要盈利2100元,每台电暖器应降价多少元?
-
(3)
该商场平均每天盈利能达到2500元吗?如果能,求出此时应降价多少;如果不能,请说明理由
-
27.
(2023九上·威远期中)
阅读材料:设a>0,b>0.∵(

)
2≥0,∴a﹣2

+

≥0,即a+

(当

=

, 即a=

时,取“=”).由此可得结论:若a>0,b>0,则当a=

时,a+

有最小值2

.
-
(1)
理解概念:若x>0,则x=
时,函数x+

有最小值为
.(写出必要步骤)
-
(2)
拓展应用:若x>1,则代数式x+

的最小值为
,此时x=
;(写出必要步骤)
-
(3)
解决问题:学校打算用篱笆围成一个长方形的生物园饲养小兔,生物园的一边AD靠墙(如图,墙足够长),面积为8m
2 , 求至少需要多少米的篱笆?
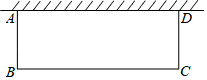
-
, 1,
,
,
,

;②
;③
.


中,D为
上一点,连结
, E为
上一点,连结
, 若
, 求证:
.
中,对角线
交于点O,E为
上一点,连结
, 若
, 求
的长.
中,对角线
交于点O,E为
中点,F为
上一点,连结
, 若
,
, 求菱形
的边长.