浙江省金华市义乌部分校2023-2024学年九年级上学期数学...

更新时间：2024-04-19 浏览次数：29 类型：月考试卷

一、选择题(本大题有10小题,每小题3分,共30分.请选出各题中一个符合题意的正确选项.不选、多选、错选均不给分)

1. (2023九上·义乌月考) 在某次班级测验中，班级的平均分为90分，小明的成绩为87分，记做-3，若小亮的成绩记做+2，则小亮的成绩为（）

A . 2分 B . 88分 C . 92分 D . 90分

答案解析收藏纠错 + 选题
2. (2023九上·婺城月考) 下列适合抽样调查的是（）

A . 了解当前全国流感的发病情况 B . 了解本班学生的视力情况 C . 旅客上飞机前的安检 D . 对组成人造卫星零部件的检查

答案解析收藏纠错 + 选题
3. (2023九上·义乌月考) 进入秋季以来，全国流感高发，其中就有甲流.已知甲流病毒的直径约为0.00000011米，用科学记数法表示0.00000011米 $\text{[math]}$ ，则 $\text{[math]}$ 为（）.

A . -6 B . -7 C . 6 D . 7

答案解析收藏纠错 + 选题
4. (2023九上·婺城月考) 有一个装有水的容器，如图所示，容器内的水面高度是10cm，现向容器内注水，并同时开始计时，在注水过程中，水面高度以每秒0.2cm的速度匀速增加，则容器注满水之前，容器内的水的体积与对应的注水时间满足的函数关系是（）.

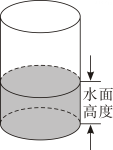
A . 正比例函数关系 B . 一次函数关系 C . 二次函数关系 D . 反比例函数关系

答案解析收藏纠错 + 选题
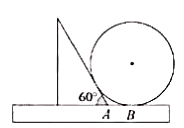
5. (2024九上·婺城期末) 如图，一把直尺， 60°的直角三角板和光盘如图摆放， A为 60°角与直尺交点， AB=3 ，则光盘的直径是（）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
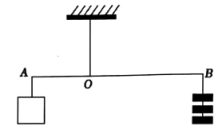
6. (2023九上·义乌月考) 在数学活动课上，兴趣小组的同学用一根质地均匀的轻质木杆和若干个钩码做实验.如图所示，在轻质木杆 $\text{[math]}$ 处用一根细线悬挂，左端 $\text{[math]}$ 处挂一重物，右端 $\text{[math]}$ 处挂钧码，每个钩码质量是50g.若 $\text{[math]}$ ，挂3个钩码可使轻质木杆水平位置平衡.设重物的质量为 $\text{[math]}$ ，根据题意列方程得（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023九上·义乌月考) 反比例函数 $\text{[math]}$ 图象上有两点 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）.

A . -1 B . 0 C . 1 D . 2

答案解析收藏纠错 + 选题
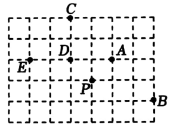
8. 如图，在正方形方格中，A，B，C，D，E，P均在格点处，则点 $\text{[math]}$ 是下列哪个三角形的外心（）.

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023九上·婺城月考) 如图所示的是中国南宋数学家杨辉在详解《九章算法》中出现的三角形状的数列，又称为“杨辉三角形”该三角形中的数据排列有着一定的规律，若将其中一组斜数列用字母a₁、a₂ ， a₃ ， …代替，如图2，则a₉₉+a₁₀₀的值为（　　）

A . 9801 B . 10000 C . 10201 D . 10500

答案解析收藏纠错 + 选题
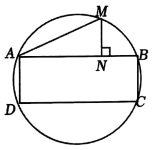
10. (2024九上·婺城期末) 如图，半径为5的圆中有一个内接矩形 $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点， $\text{[math]}$ 于点 $\text{[math]}$ ，若矩形ABCD的面积为30，则线段MN的长为（）.

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题(本大题有6小题,每小题4分,共24分.)

11. (2023九上·义乌月考) 分解因式： $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2023九上·婺城月考) 某小说分上、下各1册，小明随机将它们叠放在一起，从上到下的顺序恰好为“上册、下册”的概率是.

答案解析收藏纠错 + 选题
13. (2023九上·婺城月考) 如图，在Rt $\text{[math]}$ 中， $\text{[math]}$ ，分别以各边为直径作半圆，图中阴影部分在数学史上被称为“希波克拉底月牙”.当 $\text{[math]}$ 时，阴影部分的面积为.

答案解析收藏纠错 + 选题
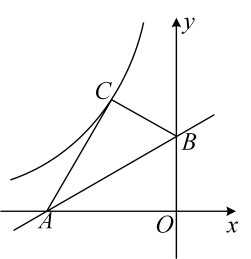
14. (2024九上·婺城期末) 如图，在平面直角坐标系中，直线 $\text{[math]}$ 经过点 $\text{[math]}$ 和 $\text{[math]}$ ，将 $\text{[math]}$ 沿直线 $\text{[math]}$ 翻折，点 $\text{[math]}$ 的对应点 $\text{[math]}$ 恰好落在反比例函数 $\text{[math]}$ 的图象上，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
15. (2023九上·义乌月考) 抛物线的函数表达式为 $\text{[math]}$ ，若将 $\text{[math]}$ 轴向下平移1个单位长度，将 $\text{[math]}$ 轴向左平移2个单位长度，则该抛物线在新的平面直角坐标系中的函数表达式为.

答案解析收藏纠错 + 选题
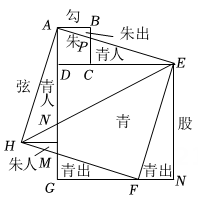
16. (2024九上·婺城期末) 魏晋时期，伟大数学家刘徽利用如图通过“以盈补虚，出入相补”的方法，即“勾自乘为朱方，股自乘为青方，令出入相补，各从其类”证明了勾股定理.已知四边形ABCD、四边形AHFE、四边形DGME均为正方形.
1. （1）若AH=13，DE=12，则 $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，则 $\text{[math]}$ .
答案解析收藏纠错 + 选题

三、解答题(本大题有8小题,共66分.)

17. (2024九上·婺城期末) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2023九上·义乌月考) 解不等式组： $\text{[math]}$ .

答案解析收藏纠错 + 选题
19. (2023九上·义乌月考) 同学们在做题时，经常用到“在直角三角形中， $\text{[math]}$ 角所对的直角边等于斜边的一半”这个定理，下面是两种添加辅助线的证明方法，请你选择一种进行证明.
已知：在 $\text{[math]}$ 中， $\text{[math]}$ ，
求证： $\text{[math]}$ .
方法一：如图1，在AB上取一点 $\text{[math]}$ ，使得 $\text{[math]}$ ，连接CD.
方法二：如图2，延长BC到 $\text{[math]}$ ，使得 $\text{[math]}$ ，连接AD.
我选择方法 ▲ .
证明：

答案解析收藏纠错 + 选题
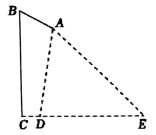
20. (2024九上·婺城期末) 如图，在路边安装路灯，灯柱BC高10m，与灯杆AB的夹角ABC为 $\text{[math]}$ .路灯采用锥形灯罩，照射范围DE长为9.8m，从D、E两处测得路灯 $\text{[math]}$ 的仰角分别为 $\text{[math]}$ .
(参考数据： $\text{[math]}$ )求：
1. （1）路灯 $\text{[math]}$ 离地面的高度(即点 $\text{[math]}$ 到地面CE的距离)；
2. （2）灯杆AB的长度.
答案解析收藏纠错 + 选题
21. (2023九上·义乌月考) 某校初三年级开展了系列交通安全知识竞赛，从中随机抽取30名学生两次知识竞赛的成绩(百分制)，并对数据(成绩)进行收集、整理、描述和分析.下面给出了部分信息.
a.这30名学生第一次竞赛成绩；
b.这30名学生两次知识竞赛的获奖情况统计表和第二次竞赛成绩得分情况统计图：（规定：分数≥90，获卓越奖；85≤分数＜90，获优秀奖；分数＜85，获参与奖）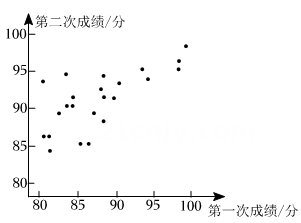

（规定：分数≥90，获卓越奖；85≤分数＜90，获优秀奖；分数＜85，获参与奖）
参与奖优秀奖卓越奖
第一次竞赛人数 10 10 10
平均分 82 87 95
第二次竞赛人数 2 12 16
平均分 84 87 93
c.第二次竞赛获卓越奖的学生成绩如下：90，90，91，91，91，91，92，93，93，94，94，94，95，95，96，98．
d.两次竞赛成绩样本数据的平均数、中位数、众数如表：
平均数中位数众数
第一次竞赛 m 87.5 88
第二次竞赛 90 n 91
根据以上信息，回答下列问题：
1. （1）小松同学第一次竞赛成绩是89分，第二次竞赛成绩是91分，在图中用“O”圈出代表小松同学的点；
2. （2）直接写出m，n的值；
3. （3）请判断第几次竞赛中初三年级全体学生的成绩水平较高，并说明理由.
答案解析收藏纠错 + 选题
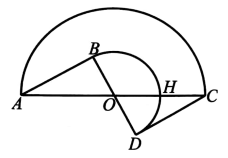
22. (2023九上·婺城月考) 如图，有两个同心半圆AC和半圆BD，其中半圆BD固定不动，半圆AC绕圆心 $\text{[math]}$ 沿顺时针方向转动一周，连接AB、CD，转动过程中，半圆BD与线段AC的交点记为点 $\text{[math]}$ ，若 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）在转动过程中，求 $\text{[math]}$ 面积的最大值；
3. （3）当AB与半圆BD相切时，求弧DH的长.
答案解析收藏纠错 + 选题
23. (2024九上·婺城期末) 在平面直角坐标系xOy中，有抛物线 $\text{[math]}$ .
1. （1）若点 $\text{[math]}$ 在抛物线上，
  ①求抛物线的对称轴；
  ②若点 $\text{[math]}$ 也在抛物线上，求 $\text{[math]}$ 的取值范围；
2. （2）当 $\text{[math]}$ 时，有已知点 $\text{[math]}$ ，若抛物线与线段AB只有一个公共点，结合函数图象，求 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题

24. (2023九上·义乌月考) 请根据素材，完成任务.

素材一	如图，在Rt $\text{[math]}$ 中， $\text{[math]}$ ，垂足为点 $\text{[math]}$ ，若保证 $\text{[math]}$ 始终为直角，则点A、B、C在以AB为直径的圆上.
素材二	如图，在Rt△ABC中， $\text{[math]}$ ，垂足为点 $\text{[math]}$ ，取AB的中点 $\text{[math]}$ ，连接OC，根据“直角三角形斜边上的中线等于斜边的一半”可知 $\text{[math]}$ ，可得OC≥CD.
素材三	如图，矩形ABCD是某实验室侧截面示意图，现需要在室内安装一块长1米的遮光板EF，且EF//AB，点 $\text{[math]}$ 到墙AB的距离为4米，到地面BC的距离为5米.点O为室内光源，OM、ON为光线， $\text{[math]}$ ，通过调节光源的位置，可以改变背光工作区的大小.若背光工作区BM+BN的和最大时，该实验室“可利用比”最高.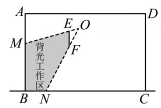
任务一	若素材一中的AB=4，求CD的最大值.
任务二	若素材二中的CD=6，求AB的最小值.
任务三	若任务二中的∠ACB=90°改成∠ACB=60°，其余条件不变，请直接写出AB的最小值.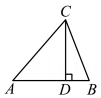
任务四	若任务二中的∠ACB=90°，CD=6改成∠ACB=α，CD=m，请直接出AB的最小值.
任务五	当素材三中的实验室“可利用比”最高，求此时BM+BN的值