一、单项选择题(本大题共6小题,每小题3分,共18分)
-
-
2.
(2023七上·南昌期中)
C919飞机是中国按照国际民航规章自行研制具有自主知识产权的大型喷气式民用飞机,最大飞行高度约为

米,标志着我国大飞机事业五人规模化系列化发展新征程.数据“

”月科学记数法表示为( )
-
-
-
A . 3
B .  C .
C .  D . 10
D . 10
-
6.
(2023七上·南昌期中)
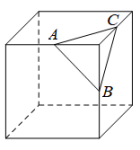
如图,在一个正方体纸盒上切一刀,切面与棱的交点分别为

,

,

, 切掉角后,将纸盒剪开展成平面,则展开图不可能是( )
二、填空题(本大题共6小题,每小题3分,共18分)
-
-
8.
(2023七上·南昌期中)
世界最大的高海拔宇宙线观测站“拉索”位于我国甘孜稻城,其海拔记为“

米”,表示高出海平面

米;全球最大的超深水半潜式钻井平台“蓝鲸2号”是我国自主设计制造的,其最大钻深记为“

米”,则“

米”表示的意义为
.
-
-
-
11.
(2023七上·南昌期中)
下列图形都是由同样大小的实心圆点按一定规律组成的,其中第①个图形一共有5个实心圆点,第②个图形一共有8个实心圆点,第③个图形一共有11个实心圆点,…,按此规律排列下去,第⑩个图形中实心圆点的个数为
.

-
三、解答题(本大题共5小题,每小题6分共30分)
-
-
(1)
计算:

.
-
(2)
化简:

.
-
-
15.
(2023七上·南昌期中)
如图,数轴上有若干个点,每相邻两点之间的距离为1,其中点A,B,C对应的数分别是整数a,b,c.

-
(1)
用含b的式子分别表示:

,

;
-
(2)
已知

, 求b的值.
-
-
(1)
请在图1的网格中画出该几何体从左面看到的形状图.
-
(2)
如果在这个几何体上再添加2个小正方体,并保持从正面看到的形状图和从左面看到的形状图不变,请在图2的网格中画出添加小正方体后的几何体从上面看到的形状图.
-
17.
(2023七上·南昌期中)
观察下列式子:
第1个式子: .
.
第2个式子: .
.
第3个式子: .
.
第4个式子: .
.
…
请你按照上述规律,回答下列问题:
-
-
-
(3)
请你按照规律计算

的值.
四、解答题(本大题共3小题,每小题8分,共24分)
-
18.
(2023七上·南昌期中)
赵老师设计了接力游戏,用合作的方式完成有理数运算,规则如下:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成运算过程如图所示:
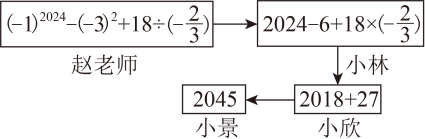
-
-
-
-
-
(2)
若

, 求F所代表的代数式的值.
-
20.
(2023七上·南昌期中)
图1是一张正方形纸片,小颖用剪刀沿虚线剪开,制作成如图2所示的新年挂图,挂图上面的小“福”是边长为a的正方形,大“福”是边长为b的正方形.

-
(1)
用含a,b的式子表示图1中正方形纸片的周长.
-
(2)
当

分米,

分米时,求小颖用剪刀剪掉部分的面积.
五、解答题(本大题共2小题,每小题9分,共18分)
-
-
(1)
求

的值.
-
(2)
计算

的值.
-
22.
(2023七上·南昌期中)
如图,长为

, 宽为

的大长方形被分割为9小块,除阴影A,B,其余7块是形状、大小完全相同的小长方形,且小长方形的宽为

.

-
(1)
由图可知,每块小长方形的长是

.
-
(2)
试说明阴影A的面积一定比阴影B的面积大

.
六、解答题(本大题共12分)
-
23.
(2023七上·南昌期中)
两个有理数在数轴上对应的点之间的距离可以用这两个数的差的绝对值表示,例如,在数轴上,有理数3与1对应的两点之间的距离为

;在数轴上,有理数5与

对应的两点之间的距离为

. 在数轴上A, B点对应的有理数分别为a,b,则可将A, B两点之间的距离表示为

或

, 记为

.

-
(1)
【解决问题】数轴上有理数

与

对应的两点之间的距离为
.
-
(2)
数轴上有理数x与

对应的两点之间的距离用含x的式子表示为
.
-
(3)
【拓展探究】如图A,B,P是数轴上的三点,点A表示的数为

, 点B表示的数为4,点P在原点处.若点P以每秒2个单位长度的速度从原点出发向右匀速运动,同时点A以每秒3个单位长度的速度向左匀速运动,点B以每秒5个单位长度的速度向右匀速运动,运动时间为t秒.求运动后

的值.
![]()
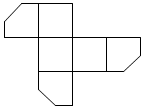 B .
B . 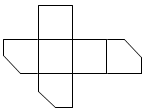 C .
C . 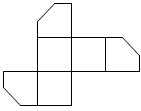 D .
D . 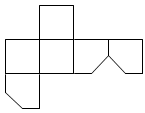


![]()

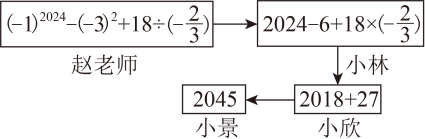

![]()