河北省沧州市泊头市2023-2024学年高一上学期1月数学期...

更新时间：2024-03-07 浏览次数：30 类型：期末考试

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符题目要求的．

1. (2024高一上·泊头期末) 已知集合 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024高一上·泊头期末) 命题“ $\text{[math]}$ ， $\text{[math]}$ ”的否定是（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024高一上·泊头期末) 已知点 $\text{[math]}$ 是角 $\text{[math]}$ 的终边上一点，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024高一上·泊头期末) 已䂑 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则a ， b ， c的大小关系为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024高一上·泊头期末) 定义在 $\text{[math]}$ 上的函数 $\text{[math]}$ 是偶函数的一个必要不充分条件为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024高一上·泊头期末) 已知 $\text{[math]}$ ， $\text{[math]}$ 是方程 $\text{[math]}$ 的两个不等实根，则 $\text{[math]}$ 的最小值是（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题
7. (2024高一上·泊头期末) 已知函数 $\text{[math]}$ ，若 $\text{[math]}$ 在 $\text{[math]}$ 上有3个零点，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024高一上·泊头期末) 已知定义在 $\text{[math]}$ 上的函数 $\text{[math]}$ ，则不等式 $\text{[math]}$ 的解集是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．

9. (2024高一上·泊头期末) 为了得到函数 $\text{[math]}$ 的图象，只需把正弦曲线上所有的点（）

A . 先向右平移 $\text{[math]}$ 个单位长度，再将横坐标缩短到原米的 $\text{[math]}$ ，纵坐标不变 B . 先向右平移 $\text{[math]}$ 个单位长度，再将横坐标伸长到原来的2倍，纵坐标不变 C . 先将横坐标缩短到原来的 $\text{[math]}$ ，纵坐标不变，再向右平移 $\text{[math]}$ 个单位长度 D . 先将横坐标伸长到原来的2倍，纵坐标不变，再向右平移 $\text{[math]}$ 个单位长度

答案解析收藏纠错 + 选题
10. (2024高一上·泊头期末) 下列说法正确的是（）

A . 若幂函数的图象经过点 $\text{[math]}$ ，则函数的解析式为 $\text{[math]}$ B . 若函数 $\text{[math]}$ ，则 $\text{[math]}$ 在区间 $\text{[math]}$ 上单调递减 C . 若正实数m ， n满足 $\text{[math]}$ ，则 $\text{[math]}$ D . 若函数 $\text{[math]}$ ，则对任意 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，有 $\text{[math]}$ $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024高一上·泊头期末) 摩天轮是一种大型转轮状的机械建筑设施，上面挂在轮边缘的是供乘客搭乘的座舱．某地一摩天轮与地面的垂直高度（最高处与地面的距离）为208米，直径193米，入口在最底部．摩天轮逆时针方向匀速转动，30分钟转一圈，假设该摩天轮共有36个座舱，且每两个座舱间隔相等，则下列说法正确的是（）

A . 若摩天轮的转速减半，则其旋转一圈的时间是原来的一半 B . 乘客从入口进入座舱，摩天轮开始转动后，乘客距离水平地面的高度 $\text{[math]}$ 米）与时间 $\text{[math]}$ （分钟）的函数解析式为 $\text{[math]}$ C . 乘客从入口进入座舱，摩天轮开始转动后，经过10分钟，乘客距离地面的高度为63.25米 D . 游客乙在游客甲后进入座舱，且中间间隔5个座舱，在摩天轮转动一周的过程中，两人距离地面的高度差的最大值为96.5米

答案解析收藏纠错 + 选题
12. (2024高一上·泊头期末) 已知函数 $\text{[math]}$ 为 $\text{[math]}$ 上的奇函数，当 $\text{[math]}$ 时， $\text{[math]}$ ，记 $\text{[math]}$ $\text{[math]}$ ，则下列结论正确的是（）

A . $\text{[math]}$ 是偶函数 B . 当 $\text{[math]}$ 时， $\text{[math]}$ C . $\text{[math]}$ 在区间 $\text{[math]}$ 上有3个零点 D . $\text{[math]}$ 大于0的零点从小到大排列依次为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， …，则 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本题共4小题，每小题5分，共20分．

13. (2024高一上·泊头期末) 已知一个扇形的圆心角为2．其周长的值等于面积的值，则扇形的半径 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2024高一上·泊头期末) 已知 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2024高一上·泊头期末) 已知函数 $\text{[math]}$ 在 $\text{[math]}$ 上单调递减，则实数 $\text{[math]}$ 的取值范围为．

答案解析收藏纠错 + 选题
16. (2024高一上·泊头期末) 若不等式 $\text{[math]}$ 对于任意 $\text{[math]}$ 恒成立，则实数 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

17. (2024高一上·泊头期末) 求下列各式的值：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2024高一上·泊头期末) 已知函数 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围；
2. （2）当 $\text{[math]}$ 时，求函数 $\text{[math]}$ 的值域．
答案解析收藏纠错 + 选题
19. (2024高一上·泊头期末) 已知 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
2. （2）求 $\text{[math]}$ 的值域．
答案解析收藏纠错 + 选题
20. (2024高一上·泊头期末) 已知函数 $\text{[math]}$ 是定义在 $\text{[math]}$ 上的奇函数．
1. （1）求 $\text{[math]}$ 的值，并判断函数 $\text{[math]}$ 的单调性（给出判断即可，不需要证明）；
2. （2）若对于任意 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，都有 $\text{[math]}$ 恒成立，求实数 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
21. (2024高一上·泊头期末) 已知函数 $\text{[math]}$ 的部分图象如图所示．
1. （1）求 $\text{[math]}$ 的解析式；
2. （2）若 $\text{[math]}$ ，是否存在实数 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，使得 $\text{[math]}$ 成立?若存在．求出 $\text{[math]}$ 的取值范围；若不存在，请说明理内．
答案解析收藏纠错 + 选题
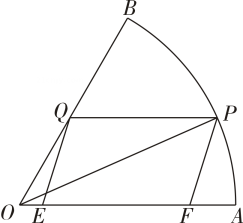
22. (2024高一上·泊头期末) 如图所示，某小区中心有一块圆心角为 $\text{[math]}$ ，半径为 $\text{[math]}$ 的扇形空地，现计划将该区域设计成亲子室外游乐区域，根据设计要求，需要铺设一块平行四边形的塑胶地面EFPQ（其中点E ， F在边OA上，点 $\text{[math]}$ 在边OB上，点 $\text{[math]}$ 在AB上），其他区域地面铺设绿地，设 $\text{[math]}$ .
1. （1） $\text{[math]}$ 表示绿地的面积 $\text{[math]}$ ；
2. （2）若铺设绿地每平分米100元，要使得铺设绿地的出用 $\text{[math]}$ 最低， $\text{[math]}$ 应取何值，并求出此时 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题