一、选择题(本大题共10小题,每小题3分,共30分.)
-
-
-
-
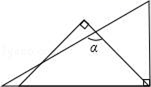
A . 60°
B . 90°
C . 108°
D . 120°
-
A . 6
B .  C .
C .  D . 9
D . 9
-
-
-
-
9.
(2023八上·哈尔滨月考)
如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于

BC的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D,连接BD.若AC=6,AD=2,则BD的长为( )

A . 2
B . 3
C . 4
D . 6
-
10.
(2023八上·长沙月考)
如图,在

中,

,

平分

交

于点

,

于点

, 则下列结论:①

平分

;②

;③

平分

;④若

, 则

. 其中正确的有( )

A . 1个
B . 2个
C . 3个
D . 4个
二、填空题(本大题共6小题,每小题3分,共18分)
-
-
-
-
-
-
16.
(2023八上·长沙月考)
如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠CPE的度数是
°.

三、计算题(本大题共9小题,第17、18、19题每题6分,第20、21题每题8分,第22、23题每题9分,第24、25题每题10分,共72分)
-
-
(1)

;
-
(2)

.
-
-
(1)

;
-
(2)

.
-
-
-
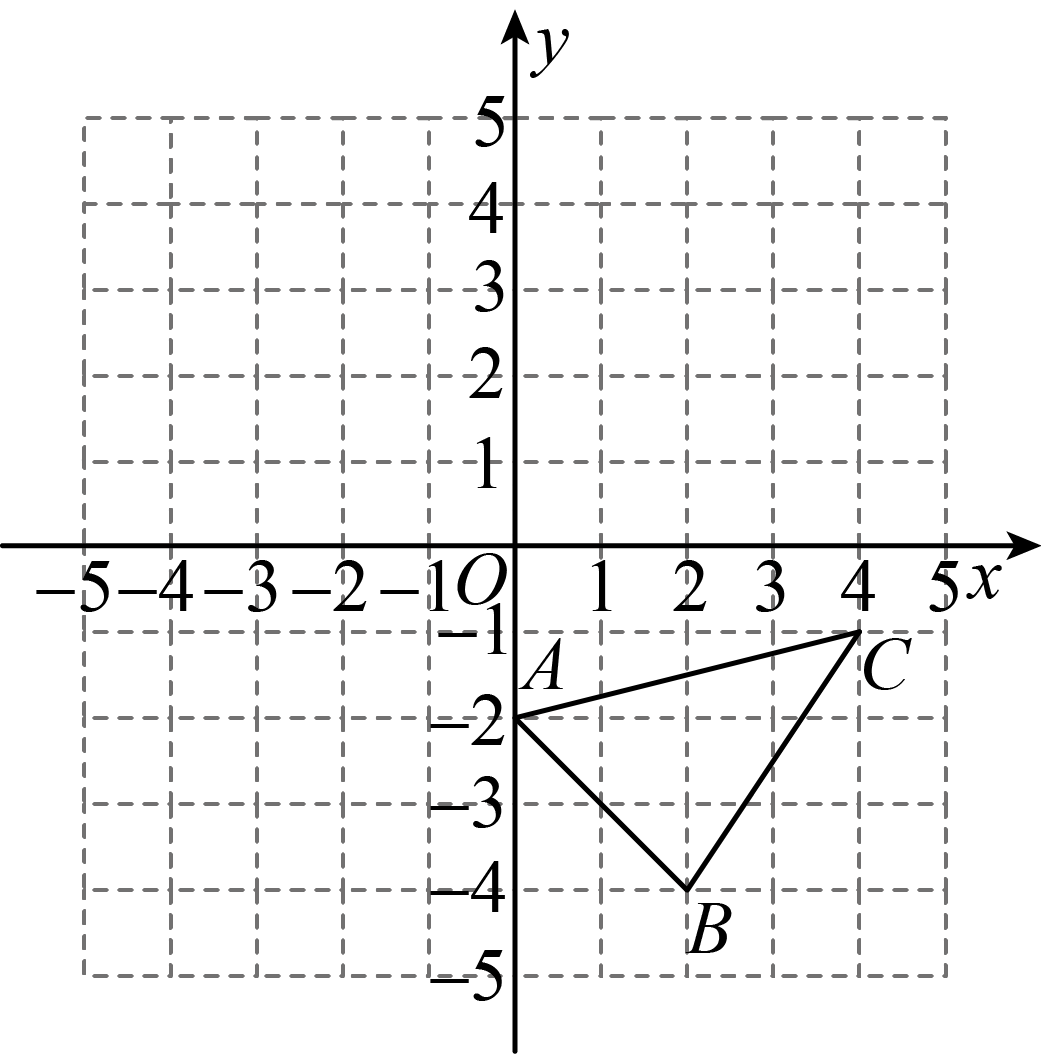
(1)
请画出

关于y轴对称的

, 并写

、

点的坐标;
-
(2)
直接写出

的面积为
;
-
(3)
在x轴上找一点P,使

的值最小,请标出点P的在坐标轴上的位置.
-
-
(1)

;
-
(2)

.
-
-
(1)
设图

中阴影部分面积为

, 图

中阴影部分面积为

, 请用含

、

的代数式表示:

,

(只需表示,不必化简);
-
(2)
以上结果可以验证哪个乘法公式?请写出这个乘法公式;
-
(3)
运用(2)中得到的公式,计算:

.
-
-
(1)
求

的度数;
-
(2)
证明

是等边三角形;
-
(3)
若

的长为2,求

的边长.
-
24.
(2023八上·长沙月考)
【阅读材料】把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法.配方法在因式分解、最值问题中都有着广泛的应用.例如:

请根据上述材料解决下列问题:
-
(1)
在横线上添上一个常数项使之成为完全平方式:

.
-
(2)
利用上述方法①进行因式分解:

.
-
(3)
参照方法②求

的最小值.
-
25.
(2023八上·长沙月考)
如图,在平面直角坐标系中,已知点
A(
a , 0)、
B(0,
b)分别为
x轴和
y轴上一点,且
a,b满足

, 过点
B作
BE⊥
AC于点
E , 延长
BE至点
D , 使得
BD=
AC , 连接
OC、
OD .

-
-
(2)
如图1,若点C在第四象限,试判断OC与OD的数量关系与位置关系,并说明理由.
-
(3)
如图2,连接
CD , 若点
C的坐标为(4,3),
CE平分∠
OCD ,
AC与
OD交于点
F .
①求D点的坐标;
②试判断DE与CF的数量关系,并说明理由.
 B .
B .  C .
C .  D .
D .