一、选择题(本大题共10小题,每小题3分,满分30分)
-
1.
(2024九下·鄞州月考)
中国古代著作《九章算术》在世界数学史上首次正式引入负数.如果盈利90元记作

元,那么亏本60元记作( )
-
2.
(2023九上·惠州期末)
第19届亚运会将于2023年9月23日至2023年10月8日在杭州举行,亚奥理事会45个成员全部报名参赛,参赛运动员人数超过

名,是史上规模最大、项目最多、覆盖面最广的一届亚运会.数据

用科学记数法表示为( )
-
-
-
5.
(2023九上·惠州期末)
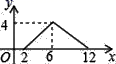
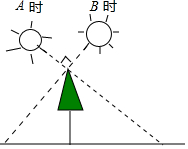
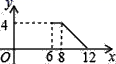
如图,小明在A时测得某树的影长为

, B时又测得该树的影长为

, 若两次日照的光线互相垂直,则树的高度为( )
-
A . 15
B . 24
C . 25
D . 48
-
A . (-1,-2)
B . (-1,2)
C . (1,-2)
D . (1,2)
-
-
9.
(2023九上·惠州期末)
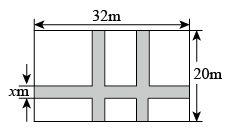
某小区计划在一块长

、宽

的长方形空地上修建三条同样宽的道路(如图),剩余的空地上种植草坪,使草坪的面积为

. 设道路的宽为

, 则下面所列方程正确的是( )
-
10.
(2023九上·惠州期末)
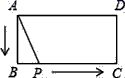
如图,矩形ABCD中,AB=2,BC=4,P为矩形边上的一个动点,运动路线是A→B→C→D→A,设P点经过的路程为x,以A,P,B为顶点的三角形面积为y,则选项图象能大致反映y与x的函数关系的是( )
二、填空题(本题共6题,每小题3分,共18分)
-
-
-
-
-
15.
(2023九上·惠州期末)
广大党员群众积极参加公益活动,据统计某市今年第一批志愿者为10万人次,第三批志愿者为12.1万人次.如果第二批、第三批志愿者人次的增长率相同,则这个增长率是
.
-
16.
(2023九上·惠州期末)
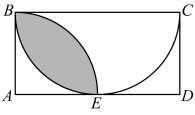
如图所示,四边形

是矩形,以

为直径作半圆与

相切于点
E , 再以点
A为圆心,线段

长为半径作弧,与

交于点
E . 若

, 则阴影部分的面积为
.(结果保留

)
三、解答题(一)(本题共3小题,每题7分,共21分)
四、解答题(二)(本题共3小题,每小题9分,共27分)
-
-
(1)
尺规作图:作对角线

的垂直平分线,分别交于

,

,

于
E ,
F ,
O;(不写作法,保留作图痕迹)
-
(2)
连接

,

, 试判断四边形

的形状,并说明理由.
-
21.
(2023九上·惠州期末)
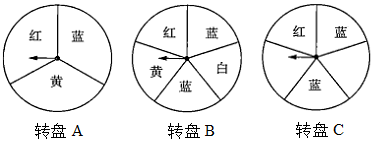
如图,三个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色小强和小亮用转盘

和转盘

做一个转盘游戏:同时转动两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,则小强获胜;若两个转盘转出的颜色相同,则小亮获胜;在其他情况下,小强和小亮不分胜负.
-
(1)
用画树状图或列表的方法表示此游戏所有可能出现的结果;
-
-
(3)
请你在转盘

的空白处,涂上适当颜色,使得用转盘

替换转盘

后,使游戏对小强和小亮是公平的(在空白处填写表示颜色的文字即可,不要求说明理由,只需给出一种结果即可).
-
22.
(2023九上·惠州期末)
为促进青少年体育运动的发展,某教育集团需要购买一批篮球和足球,已知一个篮球比一个足球的单价高

元,买两个篮球和三个足球一共需要

元.
-
-
(2)
根据实际需要,集团决定购买篮球和足球共

个,其中篮球购买的数量不少于

个,若购买篮球

个,学校购买这批篮球和足球的总费用为

(元),求

与

之间的函数关系式;
-
(3)
在(2)的条件下,由于集团可用于购买这批篮球和足球的资金最多为

元,求购买篮球和足球各多少个时,能使总费用

最小,并求出

的最小值.
五、解答题(三)(本题共2题,每题12分,共24分)
-
23.
(2023九上·惠州期末)
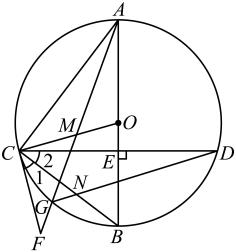
如图,在

中,直径

, 垂足为
E , 点
M在

上,

的延长线交

于点
G , 交过
C的直线于
F ,

(即:

),连接

与

交于点
N .
-
(1)
求证:

是

的切线;
-
(2)
求证:

;
-
(3)
若点
M是

的中点,

的半径长为4,

, 求

的长.
-
-
-
(2)
在

下方的抛物线上有一点
N , 过点
N作直线

轴,交

于点
M , 当点
N坐标为多少时,线段

的长度最大?最大是多少?
-
(3)
在对称轴上有一点K , 在抛物线上有一点L , 若使A , B , K , L为顶点形成平行四边形,求出K , L点的坐标.
 B .
B .  C .
C .  D .
D . 

 B .
B . 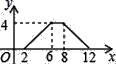 C .
C . 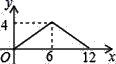 D .
D .