一、选择题(本大题共10小题,每小题3分,共30分,在每小题的四个选项中,只有一项正确)
-
A . ﹣2
B . 0
C .  D . 0.3
D . 0.3
-
A . 点动成线
B . 线动成面
C . 面动成体
D . 两点确定一条直线
-
3.
(2023七上·南海期末)
在2023年杭州亚运会的赛场上不仅有运动健儿们拼搏的英姿,更有37600多名志愿者四处奔波的动人身影,他们就像一朵朵热情洋溢的小花,阳光向上的风采.将37600用科学记数法表示应为( )
A . 0.376×105
B . 37.6×103
C . 3.76×104
D . 3.76×105
-
A . 2x﹣3=3
B . x+1=5
C . 3x+1=8
D . x﹣1=2x+2
-
A . 了解全国中学生的视力和用眼卫生情况
B . 调查市场上某种食品的色素含量是否符合国家标准
C . 检测某城市的空气质量
D . 了解全班同学每周体育锻炼的时间
-
A . 3x3﹣2x3=1
B . 2x+4x=6x2
C . 3x2y﹣3yx2=0
D . 3x+y=3xy
-
A . 6a2平方米
B . 7a2平方米
C . 8a2平方米
D . 12a2平方米
-
A . 11:15
B . 9:00
C . 6:00
D . 3:30
-
9.
(2023七上·南海期末)
某车间有15名工人,每人每天可以生产300个螺钉或800个螺母,1个螺钉配2个螺母,应安排生产螺钉和螺母的工人各多少名?设有x名工人生产螺钉,可列方程为( )
A . 2×300x=800(15﹣x)
B . 2×800x=300(15﹣x)
C . 300x=2×800(15﹣x)
D . 800x=2×300(15﹣x)
-
A . 7或8
B . 8
C . 8或9
D . 10
二、填空题(本大题共5小题,每小题3分,共15分)
-
-
12.
(2023七上·南海期末)
点A、B在数轴上,若点A表示的数是-3,点B在点A右侧,且到点A的距离等于2个单位长度,则点B所表示的数是 .
-
-
14.
(2023七上·南海期末)
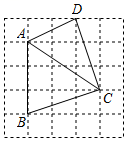
如图所示的网格是正方形网格,A,B,C,D是网格线的交点,那么∠DAC与∠ACB的大小关系为:∠DAC
∠ACB(填“>”,“=”或“<”).
-
15.
(2023七上·南海期末)
数学运算其妙无穷,小明在学习有理数时发现,存在两个有理数之和等于这两个有理数之积,如

,
请你再找两个满足以上规律且不相等的有理数, 这两个有理数可以是
.(写出一组即可)
三、解答题(一)(本大题共5小题,每小题5分,共25分)
-
-
-
18.
(2023七上·南海期末)
如图,是由6个大小相同的小立方体块搭建的几何体,请按要求在方格内分别画出从这个几何体的左面和上面看到的形状图.

-
-
20.
(2023七上·南海期末)
如图,线段AB=6,点C是线段AB的中点,使

, 延长线段BA至点E,使AE=3CD.求线段DE的长度.

四、解答题(二)(本大题共3小题,21、22题每题8分,23题10分,共26分)
-
21.
(2023七上·南海期末)
某中学为了了解本校学生每周课外阅读的时长t(单位:小时),进行了抽样调查,调查结果分为0≤t≤2、2<t≤3、3<t≤4、t>4四个等级,并依次用A、B、C、D表示,对调查结果进行统计,绘制成了如下两幅不完整的统计图,由图中给出的信息解答下列问题: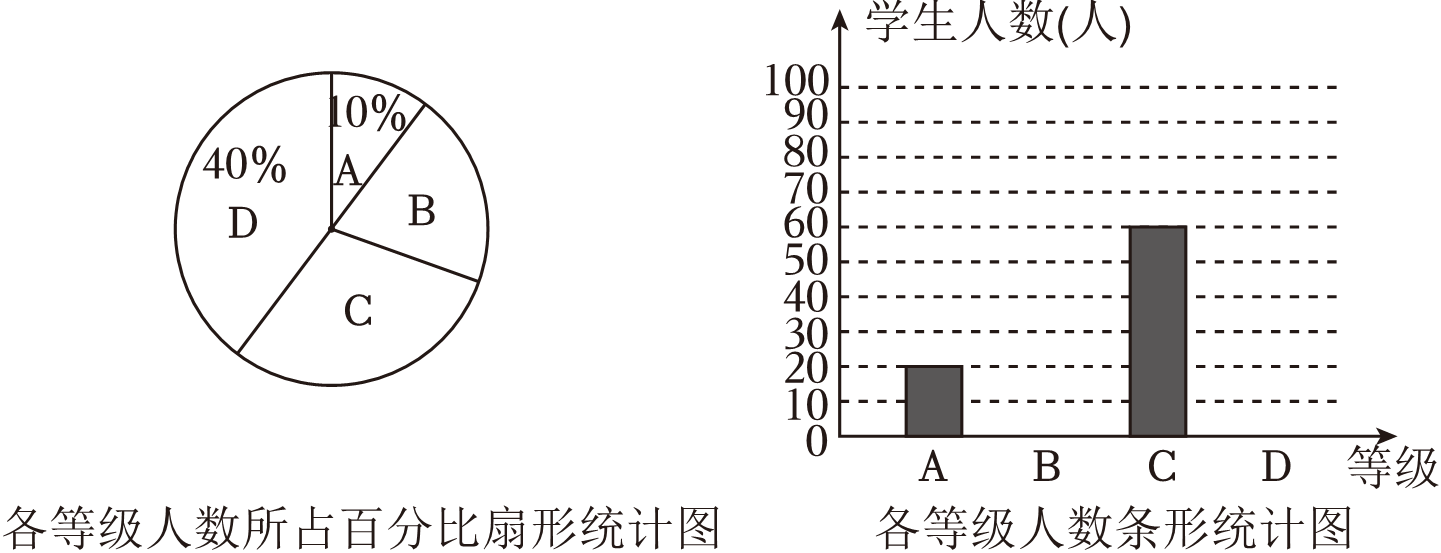
-
-
(2)
求扇形统计图中等级B所在扇形的圆心角度数,并把条形统计图补充完整;
-
(3)
若该校共有学生3000人,试估计每周课外阅读时间大于3小时的人数.
-
22.
(2023七上·南海期末)
某学校开展“请党放心,强国有我”的主题活动,准备购置A、B、C三种灯带用于舞台布置.已知A、B、C三种灯带的单价分别为15元、12元、10元.
-
(1)
当购买A、B两种灯带共20条时,设购买A种灯带x条,则购买A、B两种灯带共需要多少元?(用含x的代数式表示)
-
(2)
若学校准备购买A、B、C三种灯带共50条,一共花费640元,且购买A、B两种灯带的数量相等,则购买三种灯带各多少条?
-
23.
(2023七上·南海期末)
综合与实践
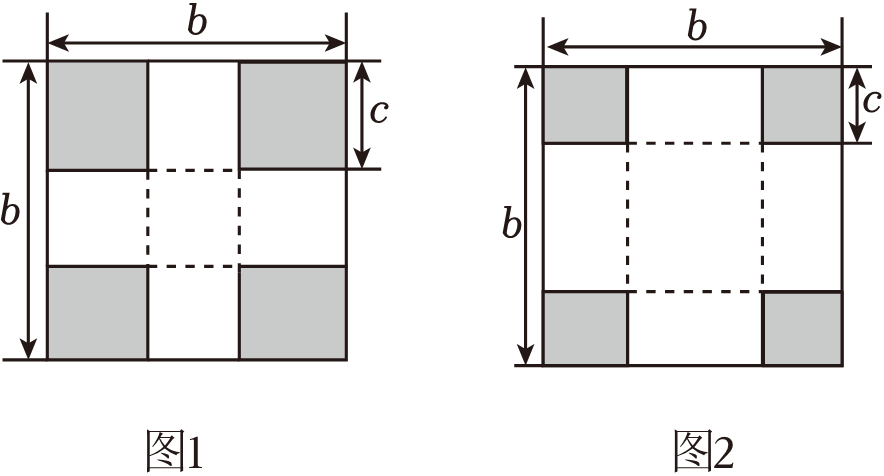
某兴趣小组利用长为a厘米,宽为b厘米的长方形纸板制作长方体纸盒,做了以下尝试:(纸板厚度及接缝处忽略不计)
-
(1)
如图1,若a=b,先在纸板四角剪去4个同样大小边长为c厘米的小正方形,再沿虚线折起来就可以做成一个无盖的正方体纸盒.此时,b与c的数量关系为 .
-
(2)
如图2,若a=b,先在纸板四角剪去4个同样大小边长为c厘米的小正方形,再沿虚线折起来就可以做成一个无盖的长方体纸盒,为了使纸盒底面更加牢固且达到废物利用的目的,将剪下的四个小正方形平铺在盒子的底面,要求既不重叠又恰好铺满.此时,b与c的数量关系为 .
-
(3)
若a=20,b=12,在纸板四角剪去4个同样大小边长为c厘米的小正方形,恰好可以制作成一个无盖的长方体纸盒.请你通过列表研究,c取何整数时,所得长方体的体积V最大?
五、解答题(三)(本大题共2小题,每小题12分,共24分)
-
24.
(2023七上·南海期末)
综合运用
将图1中的长方形纸片剪成1号、2号、3号、4号正方形和5号长方形,设1号正方形的边长为x,2号正方形的边长为y.

-
(1)
求3号、4号正方形的边长;(用含x,y的代数式表示)
-
(2)
若图1中5号长方形的周长为10,试求3号正方形的边长;
-
(3)
在第(2)问的条件下,将这5个图形按图2的方式互不重叠地放入长方形ABCD中,若阴影部分的周长为70,求长方形ABCD的周长.
-
25.
(2023七上·南海期末)
综合探究
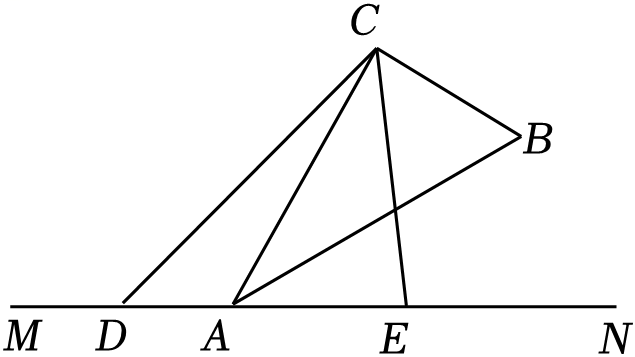
如图,在直角△ABC中,∠ACB=90°,点A在直线MN上,点D、E在直线MN上运动(点D不与点A重合),且始终满足CE平分∠BCD.
-
(1)
当点D在点A左侧时,请直接写出∠CAD与∠CAE之间的数量关系;
-
(2)
若∠CAE=60°,在点D、E运动的过程中,当△CDE是直角三角形时,求∠DCE的度数;
-
(3)
请你在以点C为顶点的角中任选一个(∠BCD、∠ACD、∠ACB除外),在点D、E运动的过程中,探究所选角与∠ACD的数量关系,并写出具体过程.



