一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的.
-
-
-
-
-
-
-
-
A . 15
B . 16
C . 17
D . 18
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
-
A . 是奇函数
B . 在区间 上单调递增
C .
上单调递增
C .  为其图象的一个对称中心
D . 最小正周期为
为其图象的一个对称中心
D . 最小正周期为
-
-
-
三、填空题:本题共4小题,每小题5分,共20分.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
-
(1)
求定义域

;
-
(2)
若“

”是“

”的充分条件,求实数

的取值范围.
-
-
-
(1)
求

的解析式;
-
(2)
解不等式

.
-
-
(1)
求函数

在

内的单调递减区间;
-
-
21.
(2024高一上·肇庆期末)
2023年9月23日,第19届亚运会开幕式在杭州举行,完美展现了“绿色”与“科技”的融合。已知绿色科技产品A在亚运会开幕式后的30天内(包括第30天),每件的销售价格为10元,日销售量

(单位:件)与第
x天的部分数据如下表所示:
x | 5 | 6 | 12 | 18 | 24 | 28 | 30 |

| 45 | 46 | 52 | 58 | 56 | 52 | 50 |
-
(1)
给出下列三个函数模型:①

;②

;③

.请你根据上表中的数据,从中选择最合适的一种函数模型来描述日销售量

与时间

的变化关系,并求出该函数的解析式及定义域.
-
(2)
若绿色科技产品B在这30天内(包括第30天)的日销售收入

(单位:元)与时间

(单位:天)的函数关系近似满足

, 求这30天内(包括第30天)绿色科技产品

的日销售收入不少于绿色科技产品

的总天数.
-
-
(1)
已知函数

, 试判断

是否为“

函数”,并说明理由;
-
(2)
已知函数

为

上的奇函数,函数


, 为其定义域上的“

函数”,求实数

的取值范围.
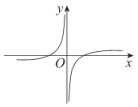 B .
B . 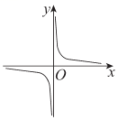 C .
C .  D .
D .