一、选择题(本题共有10小题,每小题3分,共30分)
-
-
A . 某一事件发生的可能性非常大就是必然事件
B . 概率很小的事情不可能发生
C . 2023年5月1日杭州会下雨是随机事件
D . 投掷一枚质地均匀的硬币1000次,正面朝上的次数一定是500次
-
A . sinC= B . cosC=
B . cosC= C . tanA=
C . tanA= D . sinA=
D . sinA=
-
-
A . 圆心角相等,所对的弦相等
B . 三点确定一个圆
C . 长度相等的弧是等弧
D . 弦的垂直平分线必经过圆心
-
A . 2
B . 2 C . 4
D . 2
C . 4
D . 2
-
-
8.
(2022九下·萧山月考)
若二次函数y=x
2+bx+c的图象经过点(﹣2,p),(2,q),(6,p),则p,q的大小关系为( )
A . p>q
B . p=q
C . p<q
D . p,q的大小无法比较,与b,c的取值有关
-
9.
(2022九下·萧山月考)
如图已知AB为半圆O的直径,AC,AD为弦,且AD平分∠BAC.若AB=6,AC=2,则AD的长为( )

-
10.
(2022九下·萧山月考)
已知二次函数y=(x+m-2)(x-m)+2,点A(x
1 , y
1),B(x
2 , y
2)(x
1<x
2)是其图像上两点,下列说法正确的是( )
A . 若x1+x2>2,则y1>y2
B . 若x1+x2<2,则y1>y2
C . 若x1+x2>-2,则y1>y2
D . 若x1+x2<-2,则y1<y2
二、填空题:(本题有6小题,每小题4分,共24分)
-
-
-
-
-
15.
(2022九下·萧山月考)
设函数y=(x+a)(x+b)的图像与x轴有m个交点,函数y=(ax+1)(bx+1)的图像与x轴有n个交点,写出点(m,n)所有可能的坐标是
-
16.
(2022九下·萧山月考)
如图,在矩形ABCD中,AB=6,BC=

, 点P在矩形内运动,且始终满足∠APB=150°,则DP的最小值为

三、解答题:(本题共7小题,共66分.解答应写出文字说明、证明过程或演算步骤)
-
-
(1)

-
(2)
cos245°+tan60°·sin60°
-
-
-
-
(3)
若△ABC面积为6,周长为10,则△ABC的内切圆半径为.
-
19.
(2022九下·萧山月考)
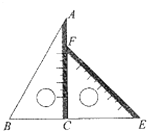
数学拓展课程《玩转学具》课堂中,小陆同学发现:一副三角板中,含45°的三角板的斜边与含30°的三角板的长直角边相等,于是,小陆同学提出一个问题:如图,将一副三角板直角顶点重合拼放在一起,点B,C,E在同一直线上,若BC=2,求AF的长.
请你运用所学的数学知识解决这个问题.
-
20.
(2022九下·萧山月考)
为迎接即将到来的3.8女神节,某超市购进一种品牌的食品,每盒进价为30元,根据往年的销售经验发现:当售价定为每盒50元时,每天可卖出100盒,每降价1元,每天可多卖出10盒,超市规定售价不低于40元/盒,不高于50元/盒.
-
(1)
求每天的销售利润W(元)与每盒降价x(元)之间的函数关系式(注明自变量的取值范围);
-
(2)
当每盒售价为多少元时,每天的销售利润最大?
-
(3)
若要使每天的销售利润不低于2090元,那么每盒的售价应定在什么范围?
-
21.
(2022九下·萧山月考)
如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB相交于点F,过点D作∠CDE=∠DFE,DE交AB的延长线于点E,过点A作⊙O的切线交ED的延长线于点G.

-
-
(2)
若tanC=

, BE=4,求AG的长.
-
22.
(2022九下·萧山月考)
如图,在

ABCD中点E在AB上,AE=

AB,ED和AC相交于点F,过点F作FG//AB,交AD于点G.

-
-
(2)
若AB:AC=

:2.
①求证:∠AEF=∠ACB;
②求证:DF2=DG·DA.
-
-
(1)
当m=0时,请判断抛物线与坐标轴的交点情况;
-
(2)
该抛物线的顶点P的位置随着m的变化而移动,当顶点P移动到最高处时,求该抛物线的顶点P的坐标;
-
(3)
已知点E(﹣1,﹣1)、F(3,7),若该抛物线与
线段EF只有一个交点,求该抛物线顶点P的横坐标

的取值范围.
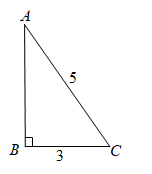

 B .
B .  C .
C .  D .
D . 





