 B .
B .  C .
C .  D .
D . 
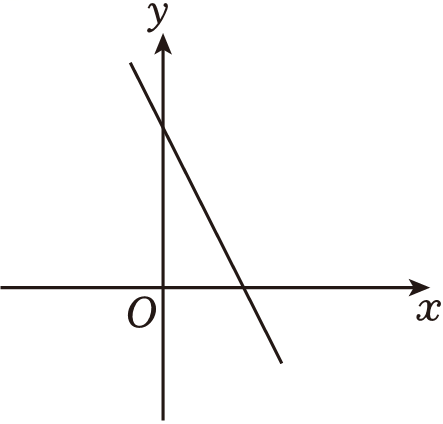





请你根据图中的信息,解答下列问题:
①线上销售方式:一律七折销售;
②线下销售方式:不超过5千克,按原价销售;超过5千克时,超出的部分每千克优惠9元;
购买水蜜桃x千克,所需费用y元,y与x之间的函数关系如图所示.

课题 | 检测新生物到皮肤的距离 | |
工具 | 医疗仪器等 | |
示意图 |
|
|
说明 | 如图2,新生物在A处,先在皮肤上选择最大限度地避开器官的B处照射新生物,检测射线与皮肤MN的夹角为∠DBN;再在皮肤上选择距离B处9cm的C处照射新生物,检测射线与皮肤MN的夹角为∠ECN. | |
测量数据 | ∠DBN=35°,∠ECN=22°,BC=9cm | |
请你根据上表中的测量数据,计算新生物A处到皮肤的距离.(结果精确到0.1cm)
(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
如何选择合适的跳台高度?

素材1 跳台滑雪是运动员借助速度和弹跳力,沿着跳台下滑,并从起跳点腾空,在空中沿抛物线飞行至着陆坡.图1是某小型跳台滑雪训练场的实物图,图2是其横截面示意图,以地面的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系,图中的抛物线C1近似表示滑雪场地上的一座小山坡,其最左端位于点O的正上方米处,最右端在水平线上,且最高点在距O点水平距离8米处.
素材2 小雪从点O正上方米处的A点滑出,滑出后沿一段抛物线C2:y=a(x−7)2+8运动.该滑雪场有若干个跳台高度不同,小山坡完全相同的训练场地,在不同场地滑行时,小雪滑行的抛物线形状不变.

小明:经过分析,得出结论:点G是线段EF的中点,且EF=2AC;
小丽:你的结论正确,若把条件“G是CF上一点,并且∠ACG=∠AGC,∠GAF=∠F”去掉,并把你的结论当成已知条件,也能完成三等分角的证明,有异曲同工之妙.
已知:ABCD是矩形,F是DA延长线上一点,点G是EF的中点,且EF=2AC;
求证:∠ECB∠ACB;

