一、单选题(共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)
-
-
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
-
A . 2,3,4
B .  ,
,  ,
,  C .
C .  ,
,  ,
,  D . 0.3,0.4,0.5
D . 0.3,0.4,0.5
-
A . 相等的角是对顶角
B . 三角形内角和为 C . 实数和数轴上点是一一对应的
D . 两条直线平行,同旁内角互补
C . 实数和数轴上点是一一对应的
D . 两条直线平行,同旁内角互补
-
5.
(2024八上·青羊期末)
甲、乙两人在相同的条件下做投篮训练,他们各投了5组,每组10次,两人投中的平均数为

, 方差

,

;则投篮的命中率较稳定的是


A . 两人一样稳定
B . 甲
C . 乙
D . 无法判断
-
-
7.
(2024八上·青羊期末)
已知直线

, 将一块含

角的直角三角板

按如图所示的方式放置,并且顶点

,

分别落在直线

,

上,若

, 则

的度数是



-
8.
(2024八上·青羊期末)
我国古代数学专著《孙子算经》中记载了一道题,“一百马,一百瓦,大马一拖三,小马三拖一,大马小马各几何?”(大意是,100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马?有多少匹小马?

设有大马

匹,小马

匹,根据题意列方程组正确的是


二、填空题(共5个小题,每小题4分,共20分,答案写在答题卡上)
-
-
-
-
-
13.
(2024八上·青羊期末)
图1是第七届国际数学教育大会

的会徽图案,它是由一串有公共顶点

的直角三角形(如图2所示)演化而成的.如果图2中的

, 那么

的长为
.

三、解答题(共6个题,共48分,解答过程写在答题卡上)
-
-
(1)

;
-
(2)

.
-
-
(1)
解方程组:

;
-
-
16.
(2024八上·青羊期末)
为了了解某学校初三年级学生每周平均课外阅读时间的情况,随机抽查了该学校初三年级
m名同学,对其每周平均课外阅读时间进行统计,绘制了如下条形统计图(图一)和扇形统计图(图二):

-
(1)
根据以上信息回答下列问题:
①求m=,并补全条形统计图.
②抽查的学生每周平均课外阅读时间这组数据的众数 小时、中位数 小时.
-
(2)
若该校共有1800名初三学生,请你估计该校学生课外阅读时间不低于3小时的人数.
-
-
(1)
在图中画出

关于

轴对称的图形△

;点

的对应点

的坐标是
▲ ;
-
(2)
求△

的面积;
-
(3)
在

中,

边上的高为
.
-
-
(1)
点

的坐标是
;直线

的函数表达式
;
-
-
(3)
点

在第二象限,当

时,动点

从点

出发,先运动到点

, 再从点

运动到点

后停止运动.点

的运动速度始终为每秒1个单位长度,运动的总时间为

(秒

, 请求出

的最小值.
四、填空题(共5个小题,每小题4分,共20分,答案写在答题卡上)
-
-
-
21.
(2024八上·青羊期末)
定义:对于给定的一次函数

、

为常数,且

, 把形如

的函数称为一次函数

的“新生函数”.已知一次函数

, 若点

在这个一次函数的“新生函数”图象上,则

的值是
;若点

在这个一次函数的“新生函数”图象上,则

的值是
.
-
22.
(2024八上·青羊期末)
如图,在

中,

,

,

, 点

,

分别是边

,

上的动点,沿

所在的直线折叠

, 使点

的对应点

始终落在边

上,若△

为直角三角形,则

的长为
.

-
23.
(2024八上·青羊期末)
如图,在等腰

中,

,

,

、

两点分别是边

、

上的动点,且

, 将线段

绕点

顺时针旋转

得到线段

, 连接

, 若

, 则线段

长度的最小值为
.

五、解答题(共3个小题,共30分,答案写在答题卡上)
-
24.
(2024八上·青羊期末)
“成都成就梦想”,第31届大运会在成都顺利举办.大运会吉祥物“蓉宝”纪念品已被商家投放市场进行试销.小冬在某网店选中

,

两款“蓉宝”玩偶,决定从该网店进货并销售.这两款“蓉宝”玩偶的进货价和销售价如表:
|  款“蓉宝”玩偶 款“蓉宝”玩偶
|  款“蓉宝”玩偶 款“蓉宝”玩偶
|
进货价(元 个) 个) | 20 | 15 |
销售价(元 个) 个) | 28 | 20 |
-
(1)
第一次小冬用550元购进了

,

两款“蓉宝”玩偶共30个,求两款“蓉宝”玩偶各购进多少个?
-
(2)
第二次小冬进货时,计划仍然购进这两款“蓉宝”玩偶共45个,网店规定

款“蓉宝”玩偶进货数量不少于20个且不超过25个,在进价和售价不变的情况下,小冬第二次销售中获得的最大利润是多少?
-
-
-
(2)
若点

, 将线段

水平向右平移

个单位

得到线段

, 连接

,

. 若△

是等腰三角形,求

的值;
-
(3)
点

为

轴上一动点,连接

, 若

, 请求出点

坐标.
-
-
(1)
问题发现:如图1,

和

均为等边三角形,当

旋转至点

,

,

在同一直线上,连接

, 易证

, 则
①线段 、
、 之间的数量关系是 ;
之间的数量关系是 ;
② ;
;
-
(2)
拓展研究:如图2,

和

均为等腰三角形,且

, 点

,

,

在同一直线上,若

,

, 求

的长度;
-
(3)
探究发现:如图3,点

为等边三角形

内一点,且

,

,

,

,

, 求

的长.
 B .
B . 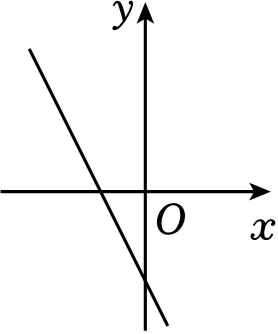 C .
C . 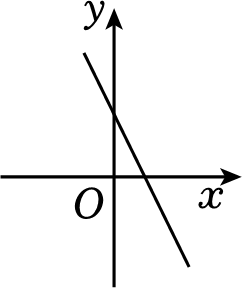 D .
D . 
, 即
,
的整数部分为2,小数部分为
.
整数部分是
, 小数部分是
, 且
, 求
的值.


、
之间的数量关系是 ;
;