2014年高考理数真题试卷（江西卷）

更新时间：2016-10-19 浏览次数：1100 类型：高考真卷

一、选择题：每小题给出的四个选项中，只有一项是符合题目要求的

1. (2014·江西理) $\text{[math]}$ 是z的共轭复数，若z+ $\text{[math]}$ =2，（z﹣ $\text{[math]}$ ）i=2（i为虚数单位），则z=（）

A . 1+i B . ﹣1﹣i C . ﹣1+i D . 1﹣i

答案解析收藏纠错 + 选题
2. (2014·江西理) 函数f（x）=ln（x²﹣x）的定义域为（）

A . （0，1） B . [0，1] C . （﹣∞，0）∪（1，+∞） D . （﹣∞，0]∪[1，+∞）

答案解析收藏纠错 + 选题
3. (2014·江西理) 已知函数f（x）=5^|x| ， g（x）=ax²﹣x（a∈R），若f[g（1）]=1，则a=（）

A . 1 B . 2 C . 3 D . ﹣1

答案解析收藏纠错 + 选题
4. (2014·江西理) 在△ABC中，内角A，B，C所对的边分别是a，b，c，若c²=（a﹣b）²+6，C= $\text{[math]}$ ，则△ABC的面积是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 3 $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2014·江西理) 一几何体的直观图如图所示，下列给出的四个俯视图中正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2024高二下·江岸期末) 某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量的关系，随机抽查了52名中学生，得到统计数据如表1至表4，则与性别有关联的可能性最大的变量是（）
表1
成绩
性别
不及格
及格
总计
男
6
14
20
女
10
22
32
总计
16
36
52
表2
视力
性别
好
差
总计
男
4
16
20
女
12
20
32
总计
16
36
52
表3
智商
性别
偏高
正常
总计
男
8
12
20
女
8
24
32
总计
16
36
52
表4
阅读量
性别
丰富
不丰富
总计
男
14
6
20
女
2
30
32
总计
16
36
52

A . 成绩 B . 视力 C . 智商 D . 阅读量

答案解析收藏纠错 + 选题
7. (2014·江西理) 阅读如图程序框图，运行相应的程序，则程序运行后输出的结果为（）

A . 7 B . 9 C . 10 D . 11

答案解析收藏纠错 + 选题
8. (2014·江西理) 若f（x）=x²+2 $\text{[math]}$ f（x）dx，则 $\text{[math]}$ f（x）dx=（）

A . ﹣1 B . ﹣ $\text{[math]}$ C . $\text{[math]}$ D . 1

答案解析收藏纠错 + 选题
9. (2014·江西理) 在平面直角坐标系中，A，B分别是x轴和y轴上的动点，若以AB为直径的圆C与直线2x+y﹣4=0相切，则圆C面积的最小值为（）

A . $\text{[math]}$ π B . $\text{[math]}$ π C . （6﹣2 $\text{[math]}$ ）π D . $\text{[math]}$ π

答案解析收藏纠错 + 选题
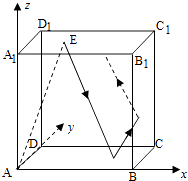
10. (2014·江西理)
如图，在长方体ABCD﹣A₁B₁C₁D₁中，AB=11，AD=7，AA₁=12．一质点从顶点A射向点E（4，3，12），遇长方体的面反射（反射服从光的反射原理），将第i﹣1次到第i次反射点之间的线段记为l_i（i=2，3，4），l₁=AE，将线段l₁ ， l₂ ， l₃ ， l₄竖直放置在同一水平线上，则大致的图形是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、选做题：请考生在下列两题中任选一题作答，在每小题给出的四个选项中，只有一项是符合题目要求的．不等式选做题

11. (2014·江西理) 对任意x，y∈R，|x﹣1|+|x|+|y﹣1|+|y+1|的最小值为（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
12. (2014·江西理) 若以直角坐标系的原点为极点，x轴的非负半轴为极轴建立极坐标系，则线段y=1﹣x（0≤x≤1）的极坐标方程为（）

A . ρ= $\text{[math]}$ ，0≤θ≤ $\text{[math]}$ B . ρ= $\text{[math]}$ ，0≤θ≤ $\text{[math]}$ C . ρ=cosθ+sinθ，0≤θ≤ $\text{[math]}$ D . ρ=cosθ+sinθ，0≤θ≤ $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题

13. (2014·江西理) 10件产品中有7件正品，3件次品，从中任取4件，则恰好取到1件次品的概率是．

答案解析收藏纠错 + 选题
14. (2014·江西理) 若曲线y=e^﹣^x上点P的切线平行于直线2x+y+1=0，则点P的坐标是．

答案解析收藏纠错 + 选题
15. (2014·江西理) 已知单位向量 $\text{[math]}$ 与 $\text{[math]}$ 的夹角为α，且cosα= $\text{[math]}$ ，向量 $\text{[math]}$ =3 $\text{[math]}$ ﹣2 $\text{[math]}$ 与 $\text{[math]}$ =3 $\text{[math]}$ ﹣ $\text{[math]}$ 的夹角为β，则cosβ=．

答案解析收藏纠错 + 选题
16. (2014·江西理) 过点M（1，1）作斜率为﹣ $\text{[math]}$ 的直线与椭圆C： $\text{[math]}$ + $\text{[math]}$ =1（a＞b＞0）相交于A，B两点，若M是线段AB的中点，则椭圆C的离心率等于．

答案解析收藏纠错 + 选题

四、解答题：解答应写出文字说明、证明过程或演算步骤

17. (2014·江西理) 已知函数f（x）=sin（x+θ）+acos（x+2θ），其中a∈R，θ∈（﹣ $\text{[math]}$ ， $\text{[math]}$ ）
1. （1）当a= $\text{[math]}$ ，θ= $\text{[math]}$ 时，求f（x）在区间[0，π]上的最大值与最小值；
2. （2）若f（ $\text{[math]}$ ）=0，f（π）=1，求a，θ的值．
答案解析收藏纠错 + 选题
18. (2014·江西理) 已知首项是1的两个数列{a_n}，{b_n}（b_n≠0，n∈N^*）满足a_nb_n+1﹣a_n+1b_n+2b_n+1b_n=0．
1. （1）令c_n= $\text{[math]}$ ，求数列{c_n}的通项公式；
2. （2）若b_n=3ⁿ^﹣¹ ，求数列{a_n}的前n项和S_n ．
答案解析收藏纠错 + 选题
19. (2014·江西理) 已知函数f（x）=（x²+bx+b） $\text{[math]}$ （b∈R）
1. （1）当b=4时，求f（x）的极值；
2. （2）若f（x）在区间（0， $\text{[math]}$ ）上单调递增，求b的取值范围．
答案解析收藏纠错 + 选题
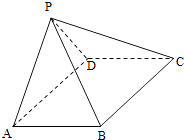
20. (2014·江西理) 如图，四棱锥P﹣ABCD中，ABCD为矩形，平面PAD⊥平面ABCD．
1. （1）求证：AB⊥PD；
2. （2）若∠BPC=90°，PB= $\text{[math]}$ ，PC=2，问AB为何值时，四棱锥P﹣ABCD的体积最大？并求此时平面BPC与平面DPC夹角的余弦值．
答案解析收藏纠错 + 选题
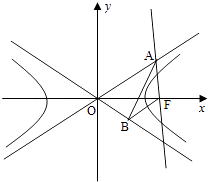
21. (2014·江西理) 如图，已知双曲线C： $\text{[math]}$ ﹣y²=1（a＞0）的右焦点为F，点A，B分别在C的两条渐近线AF⊥x轴，AB⊥OB，BF∥OA（O为坐标原点）．
1. （1）求双曲线C的方程；
2. （2）过C上一点P（x₀ ， y₀）（y₀≠0）的直线l： $\text{[math]}$ ﹣y₀y=1与直线AF相交于点M，与直线x= $\text{[math]}$ 相交于点N．证明：当点P在C上移动时， $\text{[math]}$ 恒为定值，并求此定值．
答案解析收藏纠错 + 选题
22. (2014·江西理) 随机将1，2，…，2n（n∈N^* ， n≥2）这2n个连续正整数分成A、B两组，每组n个数，A组最小数为a₁ ，最大数为a₂；B组最小数为b₁ ，最大数为b₂；记ξ=a₂﹣a₁ ， η=b₂﹣b₁ ．
1. （1）当n=3时，求ξ的分布列和数学期望；
2. （2） C表示事件“ξ与η的取值恰好相等”，求事件C发生的概率P（C）；
3. （3）对（2）中的事件C， $\text{[math]}$ 表示C的对立事件，判断P（C）和P（ $\text{[math]}$ ）的大小关系，并说明理由．
答案解析收藏纠错 + 选题