一、选择题(本大题共12小题,每小题3分,共36分.在每小题所给的四个选项中,有且只有一项是符合题目要求的)
-
1.
(2024七上·安顺期末)
安顺市年平均气温

, 历史最高气温是零上

, 最低气温是零下

. 如果历史最高气温记作

, 那么最低气温应该记作( )
-
-
A . 3
B . 2
C .  D .
D . 
-
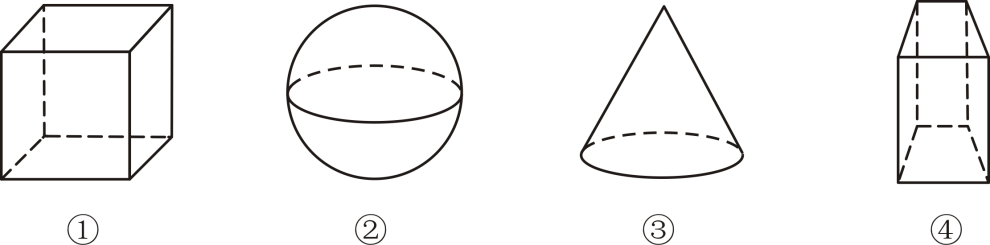
A . ①②
B . ①③
C . ②③
D . ②④
-
5.
(2024七上·安顺期末)
2023年10月26日,神舟十七号载人飞船发射取得圆满成功,航天员江新林、汤洪波、唐胜杰与神舟十六号航天员会师太空.中国空间站距离地球约400000m.数据400000用科学记数法可表示为( )
-
-
A . 南偏东 B . 南偏西
B . 南偏西 C . 北偏西
C . 北偏西 D . 北偏东
D . 北偏东
-
-
A .  B . 39
C . 41
D . 89
B . 39
C . 41
D . 89
-
10.
(2024七上·安顺期末)
A、
B、C为同一条数轴上的两点,其中点
A、C表示的数分别是2和3,且线段

, 则点
B与点
C的距离是( )
A . 4
B .  C . 4或
C . 4或 D . 4或6
D . 4或6
-
11.
(2024七上·安顺期末)
某工程队计划13天修完一条路的一部分,实际每天比原计划多修

, 不但12天完成了计划任务,而且还多修了

. 设该工程队原计划每天修路

, 则可列方程为( )
-
12.
(2024七上·安顺期末)
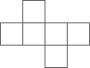
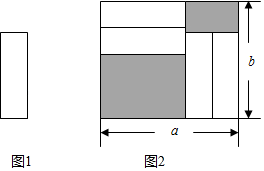
如图,把四张形状大小完全相同的小长方形卡片(如图1),不重叠地放在一个长为

、宽为

长方形内(如图2),未被卡片覆盖的部分用阴影表示,则图2中两块阴影部分的周长和是( )
二、填空题(本大题共4小题,每小题4分,共16分)
-
-
14.
已知

, 则

的补角的度数是
.
-
-
16.
(2024七上·安顺期末)
用同样大小的黑色棋子按如图所示的方式摆放,按照这样的规律摆下去,用含
n的代数式表示第
n个图形需要棋子的枚数为
.

三、解答题(本大题共9小题,共98分.解答时应写出必要的文字说明、证明过程或演算步骤)
-
-
(1)

;
-
(2)

.
-
-
(1)

;
-
(2)

.
-
-
(1)
画直线

;
-
(2)
画射线

;
-
(3)
连接

;
-
(4)
在线段

上取点

, 使

的值最小,你的依据是_▲_.
-
-
-
-
(2)
若

,

, 其他条件不变,求线段

的长.(用含

的式子表示)
-
22.
(2024七上·安顺期末)
我校七年级(3)班数学活动小组的同学用纸板制作长方体包装盒,其平面展开图和相关尺寸如下,其中阴影部分为内部粘贴角料(单位:毫米).

-
(1)
此长方体包装盒的体积为立方毫米(用含x , y的式子表示).
-
(2)
若内部粘贴角料的面积占长方体表面纸板面积的

, 则当

,

时,制作这样一个长方体共需要纸板多少平方毫米?
-
23.
(2024七上·安顺期末)
某纯净水公司每天按照顺序派车为
A ,
B ,
C ,
D ,
E ,
F ,
G ,
H八个小区运送桶装水,送水工开车从公司(原点)出发,沿公路向东西方向行驶,将水送至各小区门口.如果规定从出发点出发向东为正、向西为负.送水工某天的行驶记录如下(单位:百米):

,

,

,

,

,

,

,

.
-
(1)
送完最后一个小区后,送水工的车在出发点的什么方向?距离出发点多远?
-
(2)
若该车的耗油量为

升/千米,则该天这个送水工的车共耗油多少升?
-
24.
(2024七上·安顺期末)
某购物平台准备在春节期间举行年货节活动,此次年货节活动特别准备了
A ,

两种商品进行特价促销,已知购进了
A ,

两种商品,其中
A种商品每件的进价比

种商品每件的进价多40元,购进
A种商品2件与购进

种商品3件的进价相同.
-
(1)
求
A ,

两种商品每件的进价分别是多少元?
-
(2)
该购物平台从厂家购进了
A ,

两种商品共60件,所用资金为5800元,出售时,
A种商品在进价的基础上加价

进行标价;
B种商品按标价出售每件可获利20元.若按标价出售
A ,

两种商品,则全部售完共可获利多少元?
-
25.
(2024七上·安顺期末)
线段的计算和角的计算有紧密联系,它们之间的解法可以互相迁移.下面是某节课的学习片段,请完成探索过程:
-
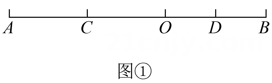
(1)
课上,老师提出问题:如图①,点
O是线段

上一点,
C、
D分别是线段

、

的中点,当

时,求线段

的长度.下面是小泽根据老师的要求进行的分析及解答过程,请你补全解答过程:
未知线段
 已知线段 …… | 因为C , D分别是线段 、 、 的中点, 的中点, 所以 , ,  , ,
 , ,
因为 , , 所以 , ,
 | 线段中点的定义 线段的和、差 等式的性质 |
-
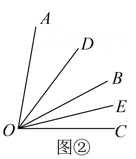
(2)
小泽举一反三,发现有些角度的计算也可以用相似的方法进行转化如图②,已知

,

是角内部的一条射线,

,

分别是

,

的平分线.求

的度数.请同学们尝试解决该问题.
-
(3)
同组的小丽同学很善于思考,她提出新的问题:如果(2)中其他条件不变,将射线

绕点
O旋转到

的外部,则

的度数是
.
 B .
B . 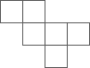 D .
D .