湖北省云学名校联盟2024学年高一下学期3月联考数学试卷

更新时间：2024-04-17 浏览次数：52 类型：月考试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. (2024高一下·湖北月考) 已知集合 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024高一下·湖北月考) 已知点O是平行四边形ABCD的对角线的交点，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024高一下·新津月考) $\text{[math]}$ 是 $\text{[math]}$ 的（）

A . 充分不必要条件 B . 必要不充分条件 C . 充要条件 D . 既不充分也不必要条件

答案解析收藏纠错 + 选题
4. (2024高一下·湖北月考) 已知幂函数 $\text{[math]}$ 是偶函数，且 $\text{[math]}$ 在 $\text{[math]}$ 上是增函数，则 $\text{[math]}$ （）

A . -2 B . -1 C . 0 D . 3

答案解析收藏纠错 + 选题
5. (2024高一下·湖北月考) 已知某物种在某特定环境下的某项指标 $\text{[math]}$ 与时间 $\text{[math]}$ （天）满足函数关系式： $\text{[math]}$ ，则在该特定环境下，至少经过（）天，该物种的该项指标不低于初始值 $\text{[math]}$ 时的100倍.（参考值： $\text{[math]}$ ）

A . 4 B . 5 C . 6 D . 7

答案解析收藏纠错 + 选题
6. (2024高一下·湖北月考) 已知函数 $\text{[math]}$ ，若函数 $\text{[math]}$ 与 $\text{[math]}$ 的图像恰有4个交点，则实数 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024高一下·湖北月考) 定义在 $\text{[math]}$ 的函数 $\text{[math]}$ 的图像位于 $\text{[math]}$ 轴上方，且是连续不断的.若 $\text{[math]}$ 的图像关于点 $\text{[math]}$ 对称，则 $\text{[math]}$ 的最小值为（）

A . $\text{[math]}$ B . 1 C . 4 D . 6

答案解析收藏纠错 + 选题
8. (2024高一下·湖北月考) 已知函数 $\text{[math]}$ ，若存在 $\text{[math]}$ ，使 $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求，全部答对的得6分，部分选对的得部分分，有选错的得0分.

9. (2024高一下·湖北月考) 若实数 $\text{[math]}$ 满足 $\text{[math]}$ ，且 $\text{[math]}$ ，则下列结论一定正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024高一下·新津月考) 已知函数 $\text{[math]}$ ，则下列说法正确的是（）

A . $\text{[math]}$ 的图像关于直线 $\text{[math]}$ 对称 B . $\text{[math]}$ 的图像的一个对称中心是 $\text{[math]}$ C . $\text{[math]}$ 在区间 $\text{[math]}$ 上单调递减 D . 若 $\text{[math]}$ 的最大值为 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为 $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024高一下·湖北月考) 函数 $\text{[math]}$ 的定义域为 $\text{[math]}$ ，且满足 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ 时， $\text{[math]}$ C . 若对任意的 $\text{[math]}$ ，都有 $\text{[math]}$ ，则 $\text{[math]}$ 的最大值为 $\text{[math]}$ D . 若函数 $\text{[math]}$ 恰有三个零点，则实数 $\text{[math]}$ 的取值范围是 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本题共3小题，每小题5分，共15分.

12. (2024高一下·湖北月考) $\text{[math]}$ .

答案解析收藏纠错 + 选题
13. (2024高一下·新津月考) 将函数 $\text{[math]}$ 的图象向左平移 $\text{[math]}$ 个单位长度后，所得函数在 $\text{[math]}$ 内不是单调函数，则 $\text{[math]}$ 的取值范围是.

答案解析收藏纠错 + 选题
14. (2024高一下·湖北月考) 已知函数 $\text{[math]}$ 的定义域为 $\text{[math]}$ ，且 $\text{[math]}$ 的图象关于点 $\text{[math]}$ 对称.若 $\text{[math]}$ ，当 $\text{[math]}$ 时，都有 $\text{[math]}$ 恒成立，则关于 $\text{[math]}$ 的不等式 $\text{[math]}$ 的解集为.

答案解析收藏纠错 + 选题

四、解答题：本题共5小题，共77分，解答应写出文字说明､证明过程或演算步骤.

15. (2024高一下·新津月考) 已知 $\text{[math]}$ 的三个内角 $\text{[math]}$ 满足： $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 的值；
2. （2）求角 $\text{[math]}$ 的大小.
答案解析收藏纠错 + 选题
16. (2024高一下·湖北月考) 已知函数 $\text{[math]}$ .
1. （1）解关于 $\text{[math]}$ 的不等式： $\text{[math]}$ ；
2. （2）命题“ $\text{[math]}$ .”是真命题，求 $\text{[math]}$ 的最大值.
答案解析收藏纠错 + 选题
17. (2024高一下·湖北月考) 学校为了鼓励学生课余时间积极参加体育锻炼，需要制定一个课余锻炼考核评分制度，建立一个每天得分 $\text{[math]}$ 与当天锻炼时间 $\text{[math]}$ （单位：分钟， $\text{[math]}$ ）的函数关系式，要求如下：
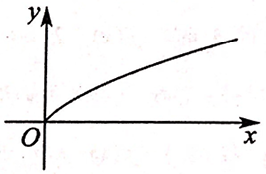
（i）函数的图象接近图示；
（ii）每天锻炼时间为0分钟时，当天得分为0分；
（iii）每天锻炼时间为9分钟时，当天得分为6分；
（iiii）每天得分最多不超过12分.
现有以下三个函数模型供选择：
① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ .
1. （1）请根据函数图象性质，结合题设条件，从中选择一个最合适的函数模型并求出解析式；
2. （2）若学校要求每天的得分不少于9分，求每天至少锻炼多少分钟？
  （参考值： $\text{[math]}$ ）
答案解析收藏纠错 + 选题
18. (2024高一下·湖北月考) 函数 $\text{[math]}$ 的部分图像如图所示，
1. （1）求函数 $\text{[math]}$ 的解析式和单调递增区间；
2. （2）将函数 $\text{[math]}$ 的图像上的各点的纵坐标保持不变，横坐标伸长为原来的2倍，得到函数 $\text{[math]}$ 的图像，若 $\text{[math]}$ 时， $\text{[math]}$ 的图像与直线 $\text{[math]}$ 恰有三个公共点，记三个公共点的横坐标分别为 $\text{[math]}$ 且 $\text{[math]}$ ，求 $\text{[math]}$ 的值
答案解析收藏纠错 + 选题
19. (2024高一下·湖北月考) 设 $\text{[math]}$ ，我们常用 $\text{[math]}$ 来表示不超过 $\text{[math]}$ 的最大整数.如： $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）解方程： $\text{[math]}$ ；
3. （3）已知 $\text{[math]}$ ，若对 $\text{[math]}$ ，使不等式 $\text{[math]}$ 成立，求实数 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题