一、选择题:本大题有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
-
2.
(2024七上·萧山期末)
2023年9月23日至10月8日,第19届亚运会在中国浙江杭州举行,亚运会主场馆为杭州奥体中心体育馆,又名“大莲花”.体育馆总建筑面积约为

平方米,将数字

用科学记数法表示为( )
-
A . 1个
B . 2个
C . 3个
D . 4个
-
A . -1
B . 0
C . 2
D . -5
-
A . 8和9之间
B . 7和8之间
C . 6和7之间
D . 5和6之间
-
6.
(2024七上·萧山期末)
如图,
P是直线
l外一点,
A ,
B ,
C三点在直线
l上,且

于点
B ,

, 则下列结论中正确的是( )
①线段 的长度是点P到直线l的距离;②线段
的长度是点P到直线l的距离;②线段 是A点到直线
是A点到直线 的距离;③在
的距离;③在 三条线段中,
三条线段中, 最短;④线段
最短;④线段 的长度是点P到直线l的距离
的长度是点P到直线l的距离

A . ①②③
B . ③④
C . ①③
D . ①②③④
-
-
8.
(2024七上·萧山期末)
古代名著《算学启蒙》中有一题:良马日行二百三十里,驽马日行一百三十里.驽马先行一十一日,问良马几何追及之?意思是:跑得快的马每天走230里,跑得慢的马每天走130里.慢马先走11天,快马几天可追上慢马?若设快马
x天可追上慢马,则可列方程为( )
-
A . 若 , 则
, 则 B . 若
B . 若 , 则
, 则 C . 若
C . 若 , 则
, 则 D . 若
D . 若 , 则
, 则
-
10.
(2024七上·萧山期末)
把四张形状、大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形的盒子底部,按图甲和图乙两种方式摆放,若长方体盒子底部的长与宽的差为2,则图甲和图乙中阴影部分周长之差为( )
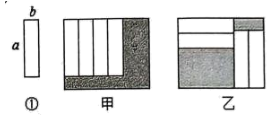
A . 4
B . 3
C . 2
D . 1
二、填空题:本大题有6个小题,每小题3分,共18分.
-
-
-
-
-
-
16.
(2024七上·萧山期末)
设代数式

, 代数式

,

为常数.观察当
x取不同值时,对应
A的值并列表如下(部分):
若 , 则
, 则 .
.
三、解答题:本大题有8个小题,共72分,解答应写出文字说明、证明过程或演算步骤.
-
-
(1)

;
-
(2)

.
-
-
(1)

;
-
(2)

.
-
-
-
(2)
在线段

上找一点
E , 使得

.
-
-
(1)
化简:

;
-
(2)
若
x是8的立方根,求

的值.
-
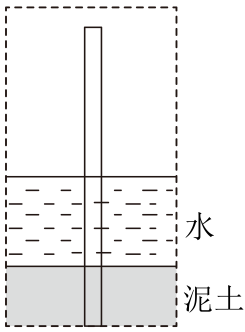
21.
(2024七上·萧山期末)
一根竹竿插入一水池底部的淤泥中(如图),竹竿的入泥部分占全长的

, 淤泥以上的入水部分比入泥部分长

米,露出水面部分为

米,竹竿有多长?水有多深?
-
-
(1)
若

, 求

的长;
-
(2)
若

是线段

的中点,若

, 求

的长(用含

的代数式表示).
-
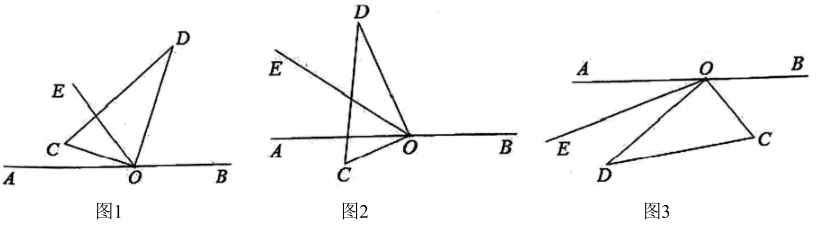
-
-
(2)
数学探究:老师提出,当三角板绕点

旋转到图2的位置时,射线

平分

, 请同学们猜想

与

之间有怎样的数量关系?并说明理由;
-
(3)
深入探究:老师提出,当三角板绕点

旋转到图3的位置时,射线

平分

, 请同学们猜想

与

之间有怎样的数量关系?并说明理由.
-
24.
(2024七上·萧山期末)
如图,在数轴上点

表示数

, 点

表示数

, 点

表示数5,点

到点

的距离记为

. 我们规定:

的大小可以用位于右边的点表示的数减去左边的点表示的数来表示.
例如: .
.

-
(1)
求线段

的长;
-
(2)
以数轴上某点

为折点,将此数轴向右对折,若点

在点

的右边,且

, 求点

表示的数;
-
(3)
若点

以每秒1个单位长度的速度向左运动,点

以每秒4个单位长度的速度向左运动,两点同时出发,经过

秒时,

, 求出

的值.
的长度是点P到直线l的距离;②线段
是A点到直线
的距离;③在
三条线段中,
最短;④线段
的长度是点P到直线l的距离

 B .
B . 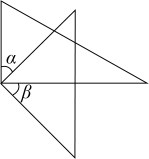 C .
C . 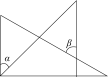 D .
D . 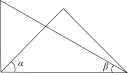

放在直线
上,
,
是三角板的两条直角边,三角板可绕点
任意旋转,射线
平分
. 当三角板绕点
旋转到图1的位置时,
, 试求
的度数;