一、选择题(本题有10小题,每题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确的选项用2B铅笔填涂在答题卡上)
-
1.
(2024九下·南山月考)
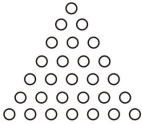
我国古代数学的许多创新与发明都曾在世界上有重要影响.下列图形“杨辉三角”“中国七巧板”“刘微割圆术”“赵爽弦图”中,是中心对称图形的是( )
-
2.
(2024九下·南山月考)
我国自主研发的C919国产大飞机商业首航取得圆满成功.C919可储存约186000升燃油,将数据186000用科学记数法表示为( )
-
3.
(2024八下·庐江期中)
一技术人员用刻度尺(单位:

)测量某三角形部件的尺寸.如图所示,已知

, 点

为边

的中点,点

、

对应的刻度为1、7,则

( )

-
-
5.
(2024·调兵山模拟)
如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心

的光线相交于点

, 点

为焦点.若

, 则

的度数为( )
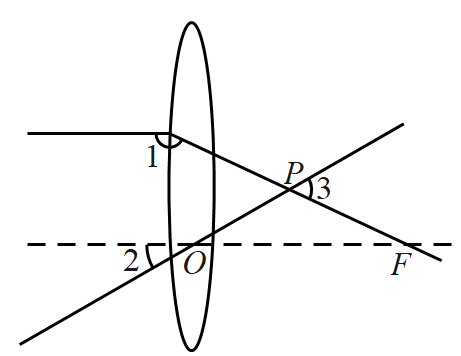
-
A . 同位角相等
B . 菱形的四条边相等
C . 正五边形的其中一个内角是72°
D . 单项式 的次数是4
的次数是4
-
7.
(2024·珠海模拟)
某校篮球队有20名队员,统计所有队员的年龄制成如下的统计表,表格不小心被滴上了墨水,看不清13岁和14岁队员的具体人数.在下列统计量,不受影响的是( )
年龄(岁) | 12岁 | 13岁 | 14岁 | 15岁 | 16岁 |
人数(个) | 2 | 
| 8 | 3 |
A . 中位数,方差
B . 众数,方差
C . 平均数,中位数
D . 中位数,众数
-
8.
(2024九下·南山月考)
元朝朱世杰所著的《算学启蒙》中,记载了这样一道题:良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之?其大意是:快马每天行240里,慢马每天行150里,慢马先行12天,快马几天可追上慢马?若设快马

天可追上慢马,由题意得( )
-
9.
(2024九下·榕城模拟)
在平面直角坐标系

中,点

,

在抛物线

(

)上,设抛物线的对称轴为直线

.若

, 则

的取值范围是( )
二、填空题:(本大题共5小题,每小题3分,共15分)
-
-
-
-
13.
(2024·南山模拟)
如图,在直角坐标系中,

与

轴相切于点

为

的直径,点

在函数

的图象上,

为

轴上一点,

的面积为6,则

的值为
.

-
三、解答题:(本题共7小题,其中第16题5分,第17题6分,第18题8分,第19题8分,第20题9分,第21题9分,第22题10分,共55分)
-
-
-
17.
(2024九下·南山月考)
劳动教育越来越受到学校的重视.某校为了初步了解学生参加家务劳动情况,对九年级学生“参加家务劳动的时间”进行了抽样调查,并将劳动时间

分为如下四组(

:

;

:

;

:

;

:

, 单位:分钟)进行统计,绘制了如下不完整的统计图.
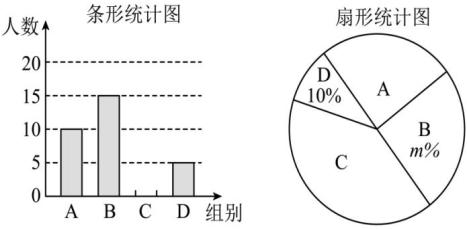
根据以上信息,解答下列问题:
-
(1)
本次抽取的学生人数一共有
人,扇形统计图中

的值为
;
-
-
(3)
已知该校九年级有600名学生,请估计该校九年级学生中参加家务劳动的时间在80分钟(含80分钟)以上的学生有多少人?
-
(4)
若

组中有3名女生,其余均是男生,从中随机抽取两名同学交流劳动感受,请用列表法或树状图法,求抽取的两名同学中恰好是一名女生和一名男生的概率.
-
18.
(2024·东莞模拟)
“低碳环保,绿色出行”成为大家的生活理念,不少人选择自行车出行.某公司销售甲、乙两种型号的自行车,其中甲型自行车进货价格为每台500元,乙型自行车进货价格为每台800元.该公司销售3台甲型自行车和2台乙型自行车,可获利650元,销售1台甲型自行车和2台乙型自行车,可获利350元.
-
(1)
该公司销售一台甲型、一台乙型自行车的利润各是多少元?
-
(2)
为满足大众需求,该公司准备加购甲、乙两种型号的自行车共20台,且资金不超过13000元,最少需要购买甲型自行车多少台?
-
19.
(2024九下·南山月考)
研究发现课堂上进行当堂检测效果很好.每节课40分钟,假设老师用于精讲的时间

(单位:分钟)与学生学习收益

的关系如图1所示,学生用于当堂检测的时间

(单位:分钟)与学生学习收益

的关系如图2所示(其中

是抛物线的一部分,

为抛物线的顶点),且用于当堂检测的时间不超过用于精讲的时间.

-
(1)
老师精讲时的学生学习收益

与用于精讲的时间

之间的函数关系式为
;
-
(2)
求学生当堂检测的学习收益

与用于当堂检测的时间

的函数关系式;
-
(3)
问“高效课堂”模式如何分配精讲和当堂检测的时间,才能使学生在这40分钟的学习收益总量

最大?(

)
-
20.
(2024九下·南山月考)
陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一.如图是从正面看到的一个“老碗”,其横截面可以近似的看成是如图(1)所示的以

为直径的半圆

,

为台面截线,半圆

与

相切于点

, 连结

与

相交于点

.水面截线

,

,

.

-
(1)
如图(1)求水深

;
-
(2)
将图(1)中的老碗先沿台面

向左作无滑动的滚动到如图(2)的位置,使得

、

重合,求此时最高点

和最低点

之间的距离

的长;
-
(3)
将碗从(2)中的位置开始向右边滚动到图(3)所示时停止,若此时

, 求滚动过程中圆心

运动的路径长.
-
21.
(2024九下·南山月考)
“转化”是解决数学问题的重要思想方法,通过构造图形全等或者相似建立数量关系是处理问题的重要手段.

-
(1)
【问题情景】:如图(1),正方形

中,点

是线段

上一点(不与点

、

重合),连接

.将

绕点

顺时针旋转90°得到

, 连接

, 求

的度数.
以下是两名同学通过不同的方法构造全等三角形来解决问题的思路,
①小聪:过点 作
作 的延长线的垂线;
的延长线的垂线;
②小明:在 上截取
上截取 , 使得
, 使得 ;
;
请你选择其中一名同学的解题思路,写出完整的解答过程.
-
(2)
【类比探究】:如图(2)点

是菱形

边

上一点(不与点

、

重合),

, 将

绕点

顺时针旋转

得到

, 使得

(

),则

的度数为
(
用含 的代数式表示
的代数式表示)
-
(3)
【学以致用】:如图(3),在(2)的条件下,连结

, 与

相交于点

, 当

时,若

, 求

的值.
 B .
B . 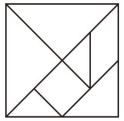 C .
C . 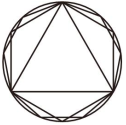 D .
D . 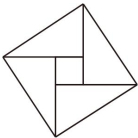



作
的延长线的垂线;
上截取
, 使得
;