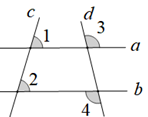
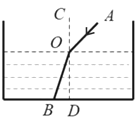
 B .
B .  C .
C .  D .
D . 
 B .
B . 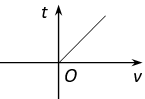 C .
C . 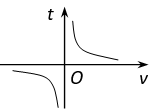 D .
D . 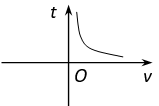
![]()
阶梯档次 | 年用电量 | 电价(单位:元/度) |
第一阶梯 | 2760度及以下部分 | 0.538 |
第二阶梯 | 2761度至4800度部分 | 0.588 |
第三阶梯 | 4801度及以上部分 | 0.838 |
小聪家去年12月份用电量为500度,电费为319元,则小聪家去年全年用电量为( )
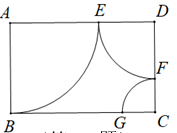
大约有多少条?
图形.它是由线段AC,线段BD,曲线AB,曲线CD围成的封闭图形,且AC//BD,BD在x轴上,曲线AB与曲线CD关于y轴对称.已知曲线CD是以C为顶点的抛物线的一部分,其函数解析式为:(p 为常数,8≤p≤40).
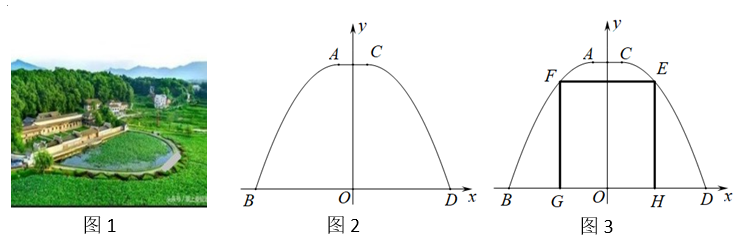
①记EF=70米时所需的塑料管总长度为L1 , EF=60米时所需的塑料管总长度为L2.若L1<L2 , 求p的取值范围.
②当EF与AC的差为多少时,三段塑料管总长度最大?请你求出三段塑料管总长度的最大值.

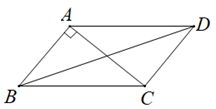
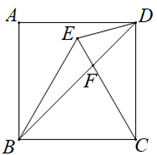
求证:.
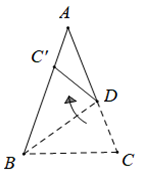
①当BC=5时,求AD的长.
②当△BCD是和美三角形时,直接写出的值.