一、单选题(本大题共12小题,每个题3分,共36分;在每小题给出的四个选项中,只有一个是符号题目要求的)
-
A . 51°34′
B . 52°34′
C . 51°74′
D . 52°74′
-
2.
(2023八下·名山月考)
对甲、乙两同学100米短跑进行5次测试,他们的成绩通过计算得

,

,

, 下列说法正确的是( )
A . 甲、乙两人的短跑成绩一样稳定
B . 乙比甲的短跑成绩稳定
C . 甲比乙的短跑成绩稳定
D . 无法确定谁的短跑成绩更稳定
-
3.
(2023八下·名山月考)
如图,A,B,C三个村庄围成了一个三角形,想在

的内部建一个超市,且超市到三个村庄的距离相等,则此超市应建在( )

A .  三条高的交点处
B .
三条高的交点处
B .  三条角平分线的交点处
C .
三条角平分线的交点处
C .  三条边垂直平分线的交点处
D .
三条边垂直平分线的交点处
D .  三条中线的交点处
三条中线的交点处
-
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
-
-
-
7.
(2023八下·名山月考)
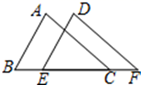
如图,在四边形
ABCD中,
BC∥
AD ,
CD⊥
AD ,
P是
CD边上的一动点,要使
PA+PB的值最小,则点
P应满足的条件是( )

A . PB=PA
B . PC=PD
C . ∠APB=90°
D . ∠BPC=∠APD
-
A . 正六边形和正方形
B . 正六边形和正三角形
C . 正五边形和正八边形
D . 正十边形和正三角形
-
A . 9
B . 16或20
C . 16
D . 20
-
10.
(2023八下·名山月考)
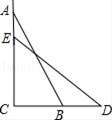
如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.5米,则梯子顶端A下落了( )米.
A . 0.5
B . 1
C . 1.5
D . 2
-
11.
(2023八下·名山月考)
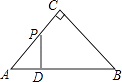
如图,△ABC是等腰直角三角形,AC=BC,AB=4,D为AB上的动点,DP⊥AB交折线A﹣C﹣B于点P,设AD=x,△ADP的面积为y,则y与x的函数图象正确的是( )
-
二、填空题(本大题共6小题,每个题4分,共24分,把答案写在题中横线上)
-
-
-
15.
(2023八下·名山月考)
如图,平行四边形
ABCD的对角线交于点
O , 且
AD≠
CD , 过点
O作
OM⊥
AC , 交
AD于
M , 如果△
CDM的周长为
a , 那么平行四边形的周长是
.

-
16.
(2023八下·名山月考)
如图,已知
AB CD
CD ,
EF⊥
AB于点
E , ∠
AEH=∠
FGH=20°,∠
H=50°,则∠
EFG的度数是
.

-
17.
(2023八下·名山月考)
在平面直角坐标系
xOy中,直线

与
x轴的交点坐标为
,与
y轴的交点坐标为
,与坐标轴所围成的三角形的面积等于
.
-
18.
(2023八下·名山月考)
如图反映了某出租公司乘车费用

元

与路程

千米

之间的关系,请你根据图中信息回答下列问题:

 公司规定的起步价是元;
公司规定的起步价是元;
 该公司规定除起步价外,超过5千米的每增加1千米多收元
该公司规定除起步价外,超过5千米的每增加1千米多收元
 若你是一名乘客,共付了44元钱,那么你的行程是千米.
若你是一名乘客,共付了44元钱,那么你的行程是千米.
三、解答题(本大题共6小题,前4题每题7分,最后两题各9分,共计46分。解答题写出必要计算过程。)
-
-
20.
(2023八下·名山月考)
如图是小明放学骑车回家行驶的路程

(千米)与行驶时间

分钟)的函数图象,已知前10分钟的速度是0.2千米分钟,行驶10分钟时车子发生故障,维修车子用了5分钟.然后又骑了5分钟到家,总共骑行了3.5千米,求最后5分钟小明的速度?

-
-
-
-
-
(2)
点

在

轴上,且

是等腰三角形,请直接写出点

的坐标.
-
-
25.
(2023八下·名山月考)
如图,

中,

,

, 点P在AB上,

, 垂足为Q.操作:画出点B关于直线PQ的对称点

, 连接

交AC于点D.以

为圆心,

长为半径画弧,交BA延长线于点E,连接

.

-
-
(2)
求

的度数;
-
(3)
若

, 求

的值(用含k的式子表示).
-
26.
(2023八下·名山月考)
已知A、B两地相距300千米,甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留1小时后,速度不变,按原路返回.设两车行驶的时间是x小时,离开A地的距离是y千米,如图是y与x的函数图象.

-
-
(2)
甲车在返程途中,两车相距20千米时,求乙车行驶的时间.

 B .
B .  C .
C .  D .
D . 



 B .
B .  C .
C . 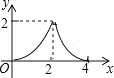 D .
D . 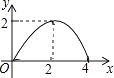


公司规定的起步价是元;
该公司规定除起步价外,超过5千米的每增加1千米多收元
若你是一名乘客,共付了44元钱,那么你的行程是千米.