一、选择题(本大题共12小题,每小题3分,共36分)
-
-
2.
(2024·万山模拟)
根据《全国文化文物和旅游统计调查制度》,结合第三方抽样调查结果初步测算,贵州省2023年国庆偎期累计接待旅客4708万人次,实现旅游收入

亿元,请将4708万用科学记数法表示为( )
-
3.
(2024·万山模拟)
某同学学习了正方体的表面展开图后,在如图所示的正方体的表面展开图上写下了“传承红色文化”六个字,还原成正方体后,“承”的对面是( )
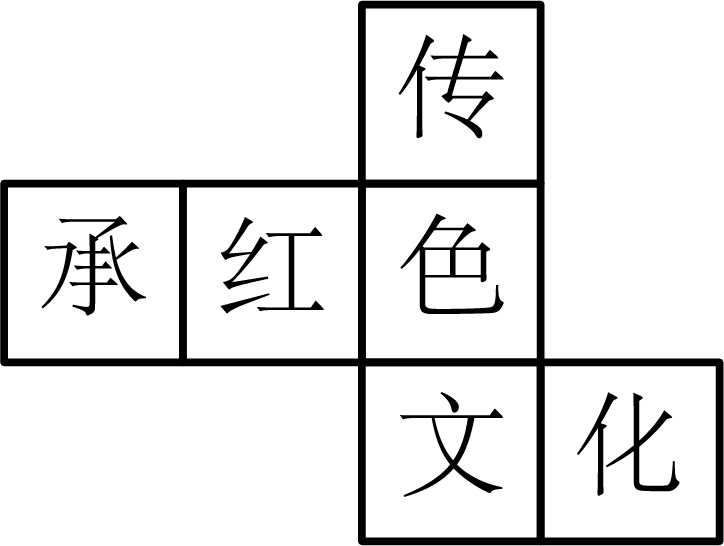
A . 传
B . 承
C . 文
D . 色
-
4.
(2024·万山模拟)
既要金山银山,又要绿水青山,贵阳市深入践行习近平总书记重要指示精神,在抓经济大开发的同时,非常重视环境保护,经过多年的不懈努力,2023年十月贵阳市的空气质量在全国省会城市排名第六名,下面是贵阳市2023年10月份某5天的空气质量指数

:43,39,20,19,32,则这组数据的中位数是( )
A . 32
B . 20
C . 39
D . 34
-
-
-
-
8.
(2024·万山模拟)
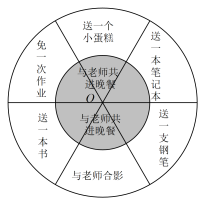
为增强班级凝聚力,吴老师组织开展了一次主题班会.班会上,他设计了一个如图的飞镖靶盘,靶盘由两个同心圆构成,小圆半径为

, 大圆半径为

, 每个扇形的圆心角为60度.如果用飞镖击中靶盘每一处是等可能的,那么小全同学任意投掷飞镖1次(击中边界或没有击中靶盘,则重投1次),投中“免一次作业”的概率是( )
-
9.
如图,用弹簧测力计将一铁块悬于盛有水的水槽中,然后匀速向上提起,使铁块完全露出水面,并上升一定高度,则下列能反映弹簧测力计的读数y(单位:N)与铁块被提起的时间x(单位:s)之间的函数关系的大致图象是( )

-
10.
(2024九下·石家庄期末)
《孙子算经》是中国古代重要的数学著作,是《算经十书》之一.书中记载了这样一个题目:今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?其大意是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺.问木长多少尺?设木长x尺,则可列方程为( )
-
-
12.
(2024·万山模拟)
如图,拋物线

(

为常数)关于直线

对称.下列五个结论:①

;②

;③

;④

;⑤

. 其中正确的有( )

A . 4个
B . 3个
C . 2个
D . 1个
二、填空题(本大题共4小题,每小题4分,共16分)
-
-
-
-
16.
(2024·万山模拟)
在平面直角坐标系中,点

、

、

、

…在x轴的正半轴上,点

、

、

…在直线

上.若点

的坐标为

, 且

、

、

…均为等边三角形.则点

的纵坐标为
.

三、解答题(本大题共9小题,共98分,解答要写出必要的文字说明、证明过程或演算步骤)
-
-
(1)
计算:

;
-
(2)
解不等式组:

-
18.
(2024·万山模拟)
2023年全国教育工作会议提出要把开展读书活动作为一件大事来抓.引导学生爱该书.读好书,善读书,贵阳市某校为了推进这项工作,对全校学生一周内平均读书时间进行抽样调查.将调查结果的数据分成A、B、C、D、E五个等级并绘制成表格和扇形统计图如下.
等级 | 周平均读书时间t(单位:小时) | 人数 |
A | 
| 4 |
B | 
| a |
C | 
| 20 |
D | 
| 15 |
E | 
| 5 |
每个等级人数扇形统计图

-
(1)
求统计图表中

,

.
-
(2)
已知该校共有2800名学生,试估计该校每周读书时间至少3小时的人数为.
-
-
19.
(2024·万山模拟)
近年来雾霾天气给人们的生活带来很大影响,空气质量问题备受人们关注.某单位计划在室内安装空气净化装置,需购进A、B两种设备.每台B种设备价格比每台A种设备价格多0.7万元,花3万元购买A种设备和花7.2万元购买B种设备的数量相同.
-
-
(2)
根据单位实际情况,需购进A、B两种设备共20台,总费用不高于15万元,求A种设备至少要购买多少台?
-
20.
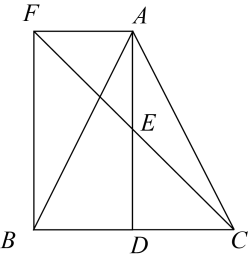
如图,在

中,D是

的中点,E是

的中点,过点A作

交

的延长线于点F.
-
(1)
求证:

;
-
-
21.
(2024·万山模拟)
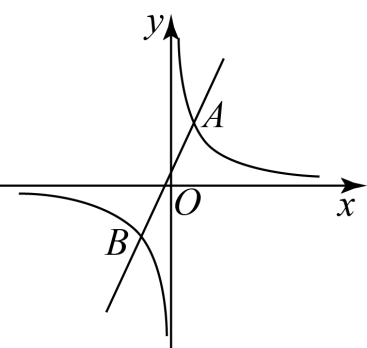
在直角坐标系中,已知

, 设函数

与函数

的图象交于点

和点

. 已知点

的横坐标是2,点

的纵坐标是

.
-
(1)
求

的值.
-
(2)
过点

作

轴的垂线,过点

作

轴的垂线,在第二象限交于点

;过点

作

轴的垂线,过点

作

轴的垂线,在第四象限交于点

. 求证:直线

经过原点.
-
22.
(2024·万山模拟)
莲花湖湿地公园是当地人民喜爱的休闲景区之一,里面的秋千深受孩子们喜爱.如图所示,秋千链子的长度为

, 当摆角

恰为

时,座板离地面的高度

为

, 当摆动至最高位置时,摆角

为

, 求座板距地面的最大高度为多少

?(结果精确到

;参考数据:

,

,

,

,

,

)

-
23.
(2024九下·淳安期中)
如图,

内接于

是⊙O的直径,过点C作

的切线交AB的延长线于点

,

,

的延长线交

于

交

于点

,

.

-
(1)
求证:

;
-
(2)
若

, 求

的半径.
-
24.
(2024·万山模拟)
排球考试要求:垫球后,球在运动中离地面的最大高度至少为2米.某次模拟测试中,某生在

处将球垫偏,之后又在A、

两处先后垫球,球沿抛物线

运动(假设抛物线

、

、

在同一平面内),最终正好在

处垫住,

处离地面的距离为1米.如图所示,以

为坐标原点1米为单位长度建立直角坐标系,

轴平行于地面水平直线

, 已知点

, 点

的横坐标为

, 抛物线

表达式为

和抛物线

表达式为

.

-
(1)
求抛物线

的函数表达式;
-
(2)
第一次垫球后,球在运动中离地面的最大高度是否达到要求?请说明理由;
-
(3)
为了使第三次垫球后,球在运动中离地面的最大高度达到要求,该生第三次垫球处

离地面的高度至少为多少米?
-
-
(1)
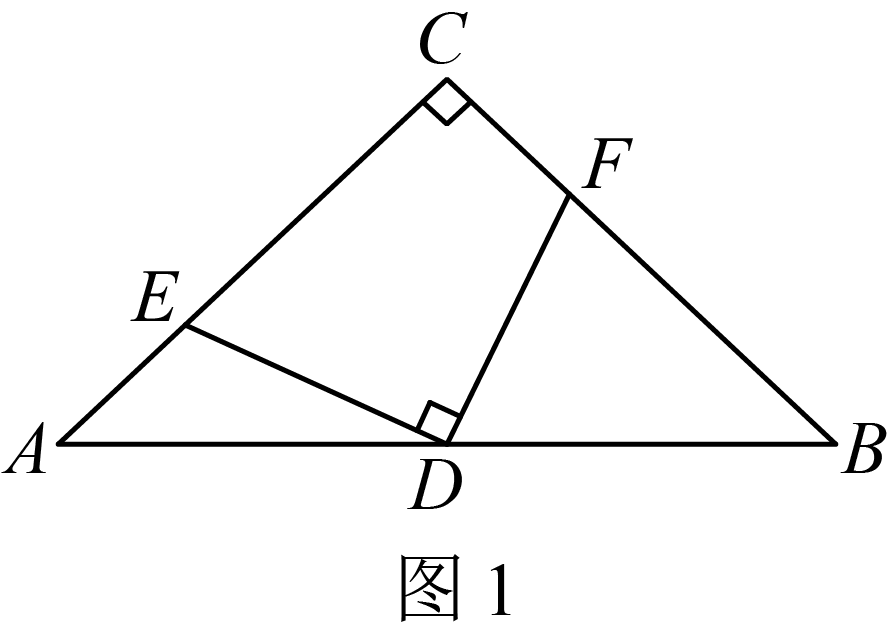
【初步感知】
如图1,当 时,兴趣小组探究得出结论:
时,兴趣小组探究得出结论: , 请写出证明过程.
, 请写出证明过程.
-
(2)
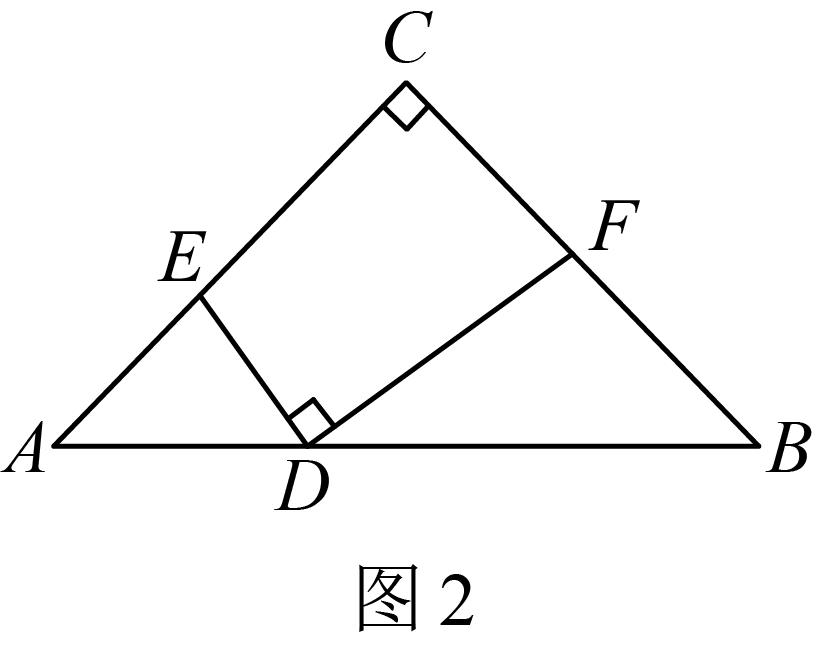
【深入探究】
如图2,当 , 且点F在线段
, 且点F在线段 上时,试探究线段
上时,试探究线段 之间的数量关系,请写出结论并证明.
之间的数量关系,请写出结论并证明.
-
(3)
【拓展运用】
请通过类比、归纳、猜想,探究出线段 之间数量关系的一般结论(直接写出结论,不必证明).
之间数量关系的一般结论(直接写出结论,不必证明).





中,
,
, D是
边上一点,且
(n为正整数),E是
边上的动点,过点D作
的垂线交直线
于点F.
时,兴趣小组探究得出结论:
, 请写出证明过程.

, 且点F在线段
上时,试探究线段
之间的数量关系,请写出结论并证明.

之间数量关系的一般结论(直接写出结论,不必证明).