一、选择题(本大题共12小题,每小题3分,共36分,在每小题给出的四个选择中,只有一项符合题目要求)
-
A . 4个
B . 3个
C . 2个
D . 1个
-
A . 五棱柱
B . 圆柱
C . 长方体
D . 五棱锥
-
3.
(2024九下·凉州模拟)
经历百年风雨,中国共产党从小到大、由弱到强,从建党时50多名党员,发展成为今天已经拥有超过9800万党员的世界第一大政党.9800万用科学记数法表示为( )
-
-
5.
如图,在直角坐标系中,

的三个顶点分别为

,

,

, 现以原点

为位似中心,在第一象限内作与

的位似比为2的位似图形

, 则顶点

的坐标是( )

-
6.
(2024九下·江北月考)
端午节又称端阳节,是中华民族重要的传统节日,我国各地都有吃粽子的习俗.某超市以10元每袋的价格购进一批粽子,根据市场调查,售价定为每袋16元,每天可售出200袋;若售价每降低1元,则可多售出80袋,问此种粽子售价降低多少元时,超市每天售出此种粽子的利润可达到1440元?若设每袋粽子售价降低

元,则可列方程为( )
-
7.
(2024·江油模拟)
如图,蒙古包可近似地看作由圆锥和圆柱组成,若用毛毡搭建一个底面圆面积为

, 圆柱高为3m,圆锥高为2m的蒙古包,则需要毛毡的面积是( )

-
8.
(2024·江油模拟)
已知

,

是关于

的一元二次方程

的两个不相等的实数根,且满足

,则

的值是( )
-
-
10.
(2024·江油模拟)
如图,

的顶点

在抛物线

上,将

绕点

顺时针旋转90°得到

, 边

与该抛物线交于点

, 则点

的坐标为( )

-
11.
(2024·江油模拟)
如图,正方形

内接于

,

为

的中点,直线

交

于点

, 如果

的半径为

, 则点

到

的距离

( )

-
12.
(2024·江油模拟)
如图,

,

, 点

在

边上(与

,

不重合),四边形

为正方形,过点

作

, 交

的延长线于点

, 连接

, 交

于点

.连接

.给出以下结论:①

;②

;③

④

.⑤

其中,正确的结论有( )个

A . 2
B . 3
C . 4
D . 5
二、填空题:(本大题共6个小题,每小题4分,共24分.)
-
-
-
15.
(2024九下·银川模拟)
“二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.若要从“立春”“立夏”“秋分”“大寒”四张邮票中抽取两张,则恰好抽到“立夏”、“秋分”两张邮票的概率是
.
-
16.
(2024·江油模拟)
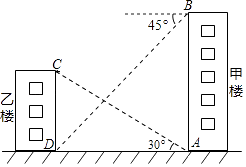
如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是120m,则乙楼的高CD是
m(结果保留根号)
-
17.
(2024·江油模拟)
如图,

、

是反比例函数

图象上的两点,过点

、

分别作

轴的平行线交

轴于点

、

, 直线

交

轴正半轴于点

.若点

的横坐标是4,

,

, 则

点的坐标是
.

-
18.
(2024·江油模拟)
如图,在矩形

中,

, 点

,

分别在边

,

上,且

,

, 将矩形沿

折叠后,点

,

分别落在

,

处,延长

交

于点

.当

,

,

三点共线时,

的面积是
.

三、解答题:(本大题共7个小题,共90分.解答应写出文字说明、证明过程或演算步骤).
-
-
(1)
计算:

-
(2)
先化简,再求值:

, 其中

.
-
20.
(2024·江油模拟)
为了解某校九年级学生的物理实验操作情况,随机抽查了40名学生实验操作的得分(满分10分).根据获取的样本数据,制作了下面的条形统计图和扇形统计图,请根据相关信息,解答下列问题.

-
(1)
这40个样本数据的平均数是分,众数是分,中位数是分;
-
(2)
扇形统计图中

的值为
;
-
(3)
若该校九年级共有480名学生,估计该校九年级物理实验操作得满分的学生有多少名.
-
-
-
(2)
请直接写出

时,

的取值范围;
-
(3)
在平面内存在一点

, 且

, 请直接写出

的最小值.
-
22.
(2024九下·娄底期中)
“文房四宝”是中国独有的书法绘画工具,即笔、墨、纸、砚,文房四宝之名,起源于南北朝时期.某中学为了落实双减政策,丰富学生的课后服务活动,开设了书法社团,计划为学生购买甲、乙两种型号“文房四宝”,经过调查得知:每套甲型号“文房四宝”的价格比每套乙型号的价格贵40元,买5套甲型号和10套乙型号共用1100元.
-
(1)
求每套甲、乙型号“文房四宝”的价格分别是多少?
-
(2)
若学校需购进甲、乙两种型号“文房四宝”共120套,总费用不超过8600元,并且根据学生需求,要求购进乙型号“文房四宝”的数量必须低于甲型号“文房四宝”数量的3倍,问有几种购买方案?最低费用是多少?
-
-
(1)
求证:

是

的切线;
-
-
-
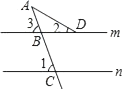
(1)
如图1,求

的大小;
-
(2)
已知点

和边

上的点

满足

,

, ①如图2,连接

, 求证:

;
②如图3,连接 , 若
, 若 ,
,  , 求
, 求 的值.
的值.
-
-
-
-
(3)
直线

与线段

相交于点

, 当

与

相似时,求点

的坐标.




, 若
,
, 求
的值.