题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

湖南省娄底市2023-2024学年九年级下学期数学期中试题

更新时间：2024-06-17 浏览次数：3 类型：期中考试

一、选择题（本大题共10个小题，每小题3分，共30分．在下列各题的四个选项中，只有一项是符合题意的）

1. (2024九下·娄底期中) 2024的倒数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2024 D . -2024

答案解析收藏纠错 + 选题
2. (2024九下·娄底期中) 流感病毒中甲型流感的致病力最强，该病毒的直径大约是0.000000086米，0.000000086这个数字用科学记数法可表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九下·娄底期中) 如图，是一个正方体的表面展开图，则原正方体中与“赢”字所在的面相对的面上标的字是（）
赢
得
中
考
胜
利

A . 中 B . 考 C . 胜 D . 利

答案解析收藏纠错 + 选题
4. (2024九下·娄底期中) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024九下·娄底期中) 已知 $\text{[math]}$ ，则 $\text{[math]}$ 的值约为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九下·娄底期中) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径，弦 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024九下·娄底期中) 反比例函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ，则下列说法错误的是（　　）

A . $\text{[math]}$ B . 函数图象分布在第二、四象限 C . 函数图象关于原点中心对称 D . 当 $\text{[math]}$ 时，y随x的增大而减小

答案解析收藏纠错 + 选题
8. (2024九下·娄底期中) 植树节的起源可以追溯到中国古代“孟春之月，盛德在木”的传统观念，这体现了古人对树木的深深敬仰．某校在“植树节”期间带领学生开展植树活动，甲、乙两班同时开始植树，甲班比乙班每小时多植3棵树，植树活动结束时，甲、乙两班同时停止植树，甲班共植70棵树，乙班共植50棵树．设甲班每小时植x棵树，依题意可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024九下·娄底期中) 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 1 B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024九下·娄底期中) 如图，抛物线 $\text{[math]}$ 与x轴交于点 $\text{[math]}$ ．点 $\text{[math]}$ ， $\text{[math]}$ 是抛物线上两点，当 $\text{[math]}$ 时，二次函数最大值记为 $\text{[math]}$ ，最小值记为 $\text{[math]}$ ，设 $\text{[math]}$ ，则m的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共8个小题，每小题3分，共24分）

11. (2024九上·良庆开学考) 若二次根式 $\text{[math]}$ 有意义，则x的取值范围是．

答案解析收藏纠错 + 选题
12. (2024九下·娄底期中) 一个多边形每个内角都是150°，则这个多边形的边数为．

答案解析收藏纠错 + 选题
13. (2024九下·娄底期中) 有一组数据：3，5，7，6，8，8，9，则这组数据的中位数是．

答案解析收藏纠错 + 选题
14. (2024九下·兰州模拟) 因式分解： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2024·武汉) 分式方程 $\text{[math]}$ 的解是．

答案解析收藏纠错 + 选题
16. (2024九下·娄底期中) 两个三角形如图摆放，其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， DE与AC交于M ，若 $\text{[math]}$ ，则 $\text{[math]}$ 大小为．

答案解析收藏纠错 + 选题
17. (2024九下·娄底期中) 如图，点A ， C在双曲线 $\text{[math]}$ 上，点B ， D在双曲线 $\text{[math]}$ 上， $\text{[math]}$ 轴，且四边形ABCD是平行四边形，则 $\text{[math]}$ 的面积为．

答案解析收藏纠错 + 选题
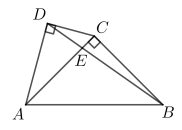
18. (2024九下·娄底期中) 如图，四边形ABCD中，∠ADC＝90°，AC⊥BC，∠ABC＝45°，AC与BD交于点E，若AB＝ $\text{[math]}$ ， CD＝2，则△ABE的面积为．

答案解析收藏纠错 + 选题

三、解答题（本大题共8小题，共66分．解答应写出文字说明，证明过程或演算步骤）

19. (2024九下·娄底期中) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2024九下·娄底期中) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ ．

答案解析收藏纠错 + 选题
21. (2024九下·娄底期中) 某校组织学生观看“天宫课堂”第二课直播，跟着空间站的翟志刚、王亚平、叶光富三位宇航员学习科学知识，他们相互配合，生动演示了四个实验：（A）微重力环境下的太空“冰雪”实验，（B）液桥演示实验，（C）水油分离实验，（D）太空抛物实验．观看完后，该校对部分学生对四个实验的喜爱情况作了抽样调查，将调查情况制成了如下的条形统计图和扇形统计图．
请根据图中信息，回答下列问题：
1. （1）共调查了名学生，图2中A所对应的圆心角度数为；
2. （2）请补全条形统计图；
3. （3）若从两名男生、两名女生中随机抽取2人参加学校组织的“我爱科学”演讲比赛，请用列表或画树状图的方法，求抽到的学生恰好是一男一女的概率．
答案解析收藏纠错 + 选题
22. (2024九下·娄底期中) 为建设美好公园社区，增强民众生活幸福感，某社区服务中心在文化活动室墙外安装避阳篷，便于社区居民休憩．如图，在侧面示意图中，遮阳篷AB长为5米，与水平面的夹角为16°，且靠墙端离地高BC为4米，当太阳光线AD与地面CE的夹角为45°时，求阴影CD的长．（结果精确到0.1米；参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
23. (2024九下·娄底期中) “文房四宝”是中国独有的书法绘画工具，即笔、墨、纸、砚，文房四宝之名，起源于南北朝时期.某中学为了落实双减政策，丰富学生的课后服务活动，开设了书法社团，计划为学生购买甲、乙两种型号“文房四宝”，经过调查得知：每套甲型号“文房四宝”的价格比每套乙型号的价格贵40元，买5套甲型号和10套乙型号共用1100元.
1. （1）求每套甲、乙型号“文房四宝”的价格分别是多少？
2. （2）若学校需购进甲、乙两种型号“文房四宝”共120套，总费用不超过8600元，并且根据学生需求，要求购进乙型号“文房四宝”的数量必须低于甲型号“文房四宝”数量的3倍，问有几种购买方案？最低费用是多少？
答案解析收藏纠错 + 选题
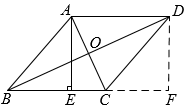
24. (2024九下·娄底期中) 如图，在菱形 $\text{[math]}$ 中，对角线 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 的垂线，垂足为点 $\text{[math]}$ ，延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是矩形；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
25. (2024九下·娄底期中) 如图，O是 $\text{[math]}$ 的外心，I是 $\text{[math]}$ 的内心，连接AI并延长交BC和 $\text{[math]}$ 于D ， E ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求AI的长．
答案解析收藏纠错 + 选题
26. (2024九下·娄底期中) 如图，抛物线C： $\text{[math]}$ 与x轴相交于A ， B两点（点A在点B的左侧），已知点B的横坐标是2，抛物线C的顶点为D ．
1. （1）求a的值及顶点D的坐标；
2. （2）点P是x轴正半轴上一点，将抛物线C绕点P旋转180°后得到抛物线 $\text{[math]}$ ，记抛物线 $\text{[math]}$ 的顶点为E ，抛物线 $\text{[math]}$ 与x轴的交点为F ， G（点F在点G的右侧）．当点P与点B重合时（如图1），求抛物线 $\text{[math]}$ 的表达式；
3. （3）如图2，在（2）的条件下，从A ， B ， D中任取一点，E ， F ， G中任取两点，若以取出的三点为顶点能构成直角三角形，我们就称抛物线 $\text{[math]}$ 为抛物线C的“勾股伴随同类函数”．当抛物线 $\text{[math]}$ 是抛物线C的勾股伴随同类函数时，求点P的坐标．
答案解析收藏纠错 + 选题

试卷信息