题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

广西壮族自治区南宁市青秀区凤岭南路中学2023-2024学年...

更新时间：2024-04-22 浏览次数：21 类型：月考试卷

一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑）

1. (2024八下·青秀月考) $\text{[math]}$ 倒数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八下·青秀月考) 我国民间，流传着许多含有吉祥意义的文字图案，表示对幸福生活的向往，良辰佳节的祝贺．比如下列图案分别表示“福”、“禄”、“寿”、“喜”，其中不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024八下·南宁月考) 生物具有遗传多样性，遗传信息大多储存在 $\text{[math]}$ 分子上，一个 $\text{[math]}$ 分子的直径约为 $\text{[math]}$ ，这个数量用科学记数法可表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024八上·石家庄月考) 下列各式是最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024八下·南宁月考) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024八下·南宁月考) 在平面直角坐标系中，点 $\text{[math]}$ 与点 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称，则点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024八下·青秀月考) 如图，平行四边形ABCD的对角线AC，BD相交于点O，下列结论错误的是（）．

A . ∠ADB＝∠CBD B . AD＝OD C . AO＝OC D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024八下·青秀月考) 如图，在 $\text{[math]}$ 中，∠ACB＝90°，∠A＝30°，BC＝4，CD是高，则AD的长为（）

A . 5 B . 6 C . 7 D . 8

答案解析收藏纠错 + 选题
9. (2024八下·南宁月考) 《九章算术》是中国古代数学名著，其中记载：每头牛比每只羊贵1两，20两买牛，15两买羊，买得牛羊的数量相等，则每头牛的价格为多少两？若设每头牛的价格为x两，则可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
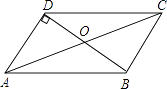
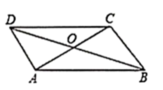
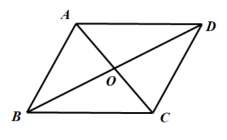
10. (2024八下·湖北期中) 如图，在平行四边形ABCD中，已知∠ODA=90°，AC=10cm，BD=6cm，则AD的长为（）

A . 4cm B . 5cm C . 6cm D . 8cm

答案解析收藏纠错 + 选题
11. (2024八下·青秀月考) 4 张长为 a、宽为 b（a＞b）的长方形纸片，按如图的方式拼成一个边长为（a＋b）的正方形，图中空白部分的面积为 S₁ ，阴影部分的面积为 S₂ ．若 S₁＝2S₂ ，则 a、b 满足（）

A . 2a＝5b B . 2a＝3b C . a＝3b D . a＝2b

答案解析收藏纠错 + 选题
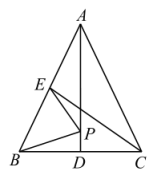
12. (2024八下·青秀月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， AD，CE是 $\text{[math]}$ 的两条中线，P是AD上的一个动点，则下列线段的长等于 $\text{[math]}$ 最小值的是（）

A . AC B . BC C . AD D . CE

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题2分，共12分）

13. (2024八下·南宁月考) 二次根式 $\text{[math]}$ 有意义的条件是.

答案解析收藏纠错 + 选题
14. (2024八下·南宁月考) 分解因式： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
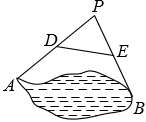
15. (2024八下·青秀月考) 如图，为测量池塘边A，B两点的距离，小军在池塘的一侧选取一点P，测得PA，PB的中点分别是D、E，且DE的长为16米，则A，B间的距离为米．

答案解析收藏纠错 + 选题
16. (2024八下·青秀月考) 如图，菱形 $\text{[math]}$ 的对角线 $\text{[math]}$ 相交于点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则菱形 $\text{[math]}$ 的面积为．

答案解析收藏纠错 + 选题
17. (2024八下·青秀月考) 如图，一架 $\text{[math]}$ 长的梯子 $\text{[math]}$ 斜靠在一竖直的墙 $\text{[math]}$ 上，这时 $\text{[math]}$ 长 $\text{[math]}$ ．如果梯子的顶端A沿墙下滑 $\text{[math]}$ ，那么梯子底端B外移m．

答案解析收藏纠错 + 选题
18. 人们把 $\text{[math]}$ 这个数叫做黄金比，著名数学家华罗庚优选法中的“0.618法”就应用了黄金比.设 $\text{[math]}$ ， $\text{[math]}$ ，记 $\text{[math]}$ ， $\text{[math]}$ ，…， $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题

三、解答题（本大题共8小题，共72分．解答应写出文字说明、证明过程或演算步骤）

19. (2024九下·乐山模拟) 计算： $\text{[math]}$ ；

答案解析收藏纠错 + 选题
20. (2024八下·南宁月考) 先化简，再求值： $\text{[math]}$ ，其中x＝ $\text{[math]}$ .

答案解析收藏纠错 + 选题
21. (2024八下·青秀月考) 如图，在平面直角坐标系中，已知 $\text{[math]}$ ． $\text{[math]}$ 关于y轴的对称图形为 $\text{[math]}$ ．
1. （1）请画出 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称的 $\text{[math]}$ ；
2. （2）若点 $\text{[math]}$ 从点 $\text{[math]}$ 处出发，向左平移 $\text{[math]}$ 个单位．当点 $\text{[math]}$ 落在 $\text{[math]}$ 内部时，直接写出 $\text{[math]}$ 的取值范围为；
3. （3）在 $\text{[math]}$ 轴上取点 $\text{[math]}$ ，使得 $\text{[math]}$ 为等腰三角形，这样的点 $\text{[math]}$ 共有个．
答案解析收藏纠错 + 选题
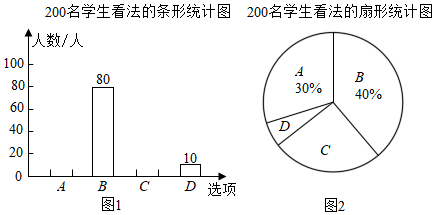
22. (2024八下·青秀月考) “生活垃圾分类”逐渐成为社会生活新风尚，某学校为了了解学生对“生活垃圾分类”的看法，随机调查了200名学生（每名学生必须选择且只能选择一类看法），调查结果分为“A.很有必要”“B.有必要”“C.无所谓”“D.没有必要”四类.并根据调查结果绘制了图1和图2两幅统计图（均不完整），请根据图中提供的信息，解答下列问题：
1. （1）补全条形统计图；
2. （2）扇形统计图中“D.没有必要”所在扇形的圆心角度数为；
3. （3）该校共有2500名学生，根据调查结果估计该校对“生活垃圾分类”认为“A.很有必要”的学生人数.
答案解析收藏纠错 + 选题
23. (2024八下·青秀月考) 如图，在四边形ABCD中，AB∥CD，AO＝CO．
1. （1）求证：四边形ABCD是平行四边形．
2. （2）若CD＝3， $\text{[math]}$ ， AC⊥AB，求四边形ABCD的面积．
答案解析收藏纠错 + 选题
24. (2024八下·青秀月考) 某市为创建全国文明城市，开展“美化绿化城市”活动，计划经过若干年使城区绿化总面积新增360万平方米．自2018年初开始实施后，实际每年绿化面积是原计划的1.5倍，这样可提前4年完成任务．
1. （1）实际每年绿化面积为多少万平方米？
2. （2）为加大创建力度，市政府决定从2021年起加快绿化速度，要求不超过3年完成，那么实际平均每年绿化面积至少还要增加多少万平方米？
答案解析收藏纠错 + 选题
25. (2024八下·青秀月考) 先阅读下面的内容，再解决问题：
古希腊的几何学家海伦（ $\text{[math]}$ ，约公元50年），在数学史上以解决几何测量问题而闻名．在他的著作《度量》一书中，证明了如下结论：如果一个三角形三边长分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，记 $\text{[math]}$ ，那么三角形的面积为 $\text{[math]}$ ．这一公式称为海伦公式．
1. （1）已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的三边长，满足 $\text{[math]}$ ，求 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的值．
2. （2）请你用海伦公式求 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
26. (2024八下·青秀月考) 【教材呈现】下图是华师版八年级下册数学教材第121页的部分内容．
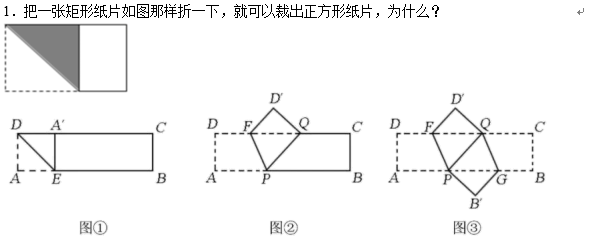
1. （1）【问题解决】如图①，已知矩形纸片 $\text{[math]}$ ，将矩形纸片沿过点 $\text{[math]}$ 的直线折叠，使点 $\text{[math]}$ 落在边 $\text{[math]}$ 上，点 $\text{[math]}$ 的对应点为 $\text{[math]}$ ，折痕为 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上．求证：四边形 $\text{[math]}$ 是正方形．
2. （2）【规律探索】由【问题解决】可知，图①中的 $\text{[math]}$ 为等腰三角形．现将图①中的点 $\text{[math]}$ 沿 $\text{[math]}$ 向右平移至点 $\text{[math]}$ 处（点 $\text{[math]}$ 在点 $\text{[math]}$ 的左侧），如图②，折痕为 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上，点 $\text{[math]}$ 在 $\text{[math]}$ 上，那么 $\text{[math]}$ 还是等腰三角形吗？请说明理由．
3. （3）【结论应用】在图②中，当 $\text{[math]}$ 时，将矩形纸片继续折叠如图③，使点 $\text{[math]}$ 与点 $\text{[math]}$ 重合，折痕为 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上．要使四边形 $\text{[math]}$ 为菱形，则 $\text{[math]}$ ．
答案解析收藏纠错 + 选题

试卷信息