题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

湖北省内地西藏班（校）2023-2024学年八年级下学期期中...

更新时间：2024-05-26 浏览次数：7 类型：期中考试

一、选择题：（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的，不选，错选或多选均不得分）

1. (2024八下·湖北期中) 若式子 $\text{[math]}$ 有意义，则 $\text{[math]}$ 的取值范围是（　　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八下·湖北期中) 下列各式中，属于最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024八下·湖北期中) 下列各组数中能作为直角三角形的三边长的是（　　）

A . 1，1， $\text{[math]}$ B . 1， $\text{[math]}$ ， 2 C . 2，3，4 D . 5，6，7

答案解析收藏纠错 + 选题
4. (2024八下·湖北期中) 下列说法错误的是（　　）

A . 对角线互相平分的四边形是平行四边形 B . 两组对边分别相等的四边形是平行四边形 C . 一组对边平行且相等的四边形是平行四边形 D . 一组对边相等，另一组对边平行的四边形是平行四边形

答案解析收藏纠错 + 选题
5. (2024八下·永定期中) 如图，将平行四边形 $\text{[math]}$ 的一边 $\text{[math]}$ 延长至点E ，若 $\text{[math]}$ ，则 $\text{[math]}$ （　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024八下·湖北期中) 下列选项中的运算正确的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024八下·南宁期中) 如图，平行四边形ABCD的对角线AC ， BD相交于点O ，下列说法正确的是 (　　)

A . ∠ABD=∠CBD　　　　 B . ∠BAD=2∠ABC C . OB=OD　　　　 D . OD=AD

答案解析收藏纠错 + 选题
8. (2024八下·湖北期中) 在平面直角坐标系的第二象限内有一点M ，点M到x轴距离为3，到原点距离为5，则点M的坐标是（　　）

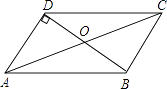
A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024八下·湖北期中) 如图，在平行四边形ABCD中，已知∠ODA=90°，AC=10cm，BD=6cm，则AD的长为（）

A . 4cm B . 5cm C . 6cm D . 8cm

答案解析收藏纠错 + 选题
10. (2024八下·湖北期中) 如图，点P是以A为圆心，AB为半径的圆弧与数轴的交点，则数轴上点P表示的实数是（）

A . -2 B . -2.2 C . - $\text{[math]}$ D . - $\text{[math]}$ +1

答案解析收藏纠错 + 选题
11. (2024八下·湖北期中) 如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙的距离为0.7米，顶端距离地面2.4米．若保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面1.5米，则小巷的宽度为（）

A . 1.8米 B . 2米 C . 2.5米 D . 2.7米

答案解析收藏纠错 + 选题
12. (2024八下·乌鲁木齐期中) 如图，菱形 $\text{[math]}$ 的对角线 $\text{[math]}$ 相交于点 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 边上一动点（不与点 $\text{[math]}$ 重合）， $\text{[math]}$ 于点 $\text{[math]}$ 点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为（）

A . 3 B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题3分，共18分）

13. (2024八下·湖北期中) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2024八下·湖北期中) 如图所示， $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2024八下·合浦期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， D是 $\text{[math]}$ 的中点．若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2024八下·湖北期中) 已知 $\text{[math]}$ 是整数，则正整数n的最小值为．

答案解析收藏纠错 + 选题
17. (2024八下·湖北期中) 如图所示，已知圆柱的底面周长为36，高 $\text{[math]}$ ， $\text{[math]}$ 点位于圆周顶面 $\text{[math]}$ 处，小虫在圆柱侧面爬行，从 $\text{[math]}$ 点爬到 $\text{[math]}$ 点，然后再爬回 $\text{[math]}$ 点，则小虫爬行的最短路程为．

答案解析收藏纠错 + 选题
18. (2024八下·湖北期中) 观察分析下列数据：0，－ $\text{[math]}$ ， $\text{[math]}$ ，－3，2 $\text{[math]}$ ，－ $\text{[math]}$ ，3 $\text{[math]}$ ，…，根据数据排列的规律得到第16个数据应是．(结果需化简)

答案解析收藏纠错 + 选题

三、解答题（本大题共9小题，共66分，解答应写出必要的文字说明、证明过程或演算步骤．）

19. (2023九上·广州开学考) 计算：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
20. (2024八下·湖北期中) 在 $\text{[math]}$ 中， $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
21. (2024八下·湖北期中) 先化简，再求值： $\text{[math]}$ ，从 $\text{[math]}$ 1中选择一个你最喜欢的整数代入计算．

答案解析收藏纠错 + 选题
22. (2024八下·湖北期中) 如图，在矩形 $\text{[math]}$ 中，点E ， F在BC上，且 $\text{[math]}$ ，连接 $\text{[math]}$ ．求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
23. (2024八下·湖北期中) 如图，从一个大正方形中裁去面积为 $\text{[math]}$ 和 $\text{[math]}$ 的两个小正方形，求留下部分的面积．

答案解析收藏纠错 + 选题
24. (2024八下·湖北期中) 如图，点E、F在线段BC上，AB＝CD，BE＝CF且∠B＝∠C.
1. （1）求证：△ABF≌△DCE；
2. （2）请猜想四边形AEDF的形状，并加以证明.
答案解析收藏纠错 + 选题
25. (2024八下·湖北期中) 如图，在矩形 $\text{[math]}$ 中，点E，F分别在边 $\text{[math]}$ 上， $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 相交于点G．求证：矩形 $\text{[math]}$ 为正方形；

答案解析收藏纠错 + 选题
26. (2024八下·湖北期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 的平分线交 $\text{[math]}$ 于点D ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）试判断四边形 $\text{[math]}$ 的形状，并说明理由；
2. （2）若 $\text{[math]}$ ，且 $\text{[math]}$ ，求四边形 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
27. (2024八下·湖北期中) 在 $\text{[math]}$ ABCD中，AC、BD交于点O ，过点O作直线EF、GH ，分别交平行四边形的四条边于E、G、F、H四点，连结EG、GF、FH、HE ．
1. （1）如图①，试判断四边形EGFH的形状，并说明理由；
2. （2）如图②，当EF⊥GH时，四边形EGFH的形状是；
3. （3）如图③，在（2）的条件下，若AC=BD ，四边形EGFH的形状是；
4. （4）如图④，在（3）的条件下，若AC⊥BD ，试判断四边形EGFH的形状，并说明理由．
答案解析收藏纠错 + 选题

试卷信息