一、选择题(本大题共10小题,每小题3分,共30分)
-
A . 2
B .  C .
C .  D . -2
D . -2
-
-
3.
(2024·江门模拟)

将推出基于

的自有聊天机器人,最终目标让

的7.5亿月活跃用户都可以使用该机器人. 其中7.5 亿用科学记数法表示为( )
-
-
5.
(2024·江门模拟)
某小组英语听力口语考试的分数依次为:25,29,27,25,22,30,26,这组数据的中位数是( )
A . 27
B . 26
C . 25.5
D . 25
-
A . 1
B .  C . 0
D . 3
C . 0
D . 3
-
-
A . 3
B . 9
C . 10
D . 15
-
9.
(2024·江门模拟)
如图,AB为半圆O的直径,C为半圆上的一点,OD⊥AC,垂足为D,延长OD与半圆O交于点E.若AB=8,∠CAB=30°,则图中阴影部分的面积为( )
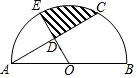
-
10.
(2024·江门模拟)
如图,矩形
OABC的面积为36,它的对角线
OB与双曲线
y 
相交于点
D , 且
OD:
OB=2:3,则
k的值为( )
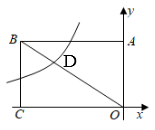
A . 12
B . ﹣12
C . 16
D . ﹣16
二、填空题(本大题共5小题,每小题3分,共15分)
-
-
-
-
14.
(2024·江门模拟)
如图,是小明设计用手电来测量某古城墙高度的示意图,点

处放一水平的平面镜,光线从点

出发经平面镜反射后刚好射到古城墙

的顶端

处,已知

, 且测得

, 那么该古城墙的高度是

.

-
15.
(2024·江门模拟)
若三个边长为1的正方形按如图的方式放在

内,其中
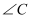
为直角,
D ,
E两点都是正方形的顶点,点
D在

边上,点
E在线段

上,则斜边

的长为
.

三、解答题(一)(本大题共3小题,第16题10分, 第 17、18 题各7分,共24分)
-
-
(1)
计算:

-
(2)
先化简, 再求值:

其中

.
-
-
(1)
用尺规在边AB上求作一点P,使PC=PB,并连接PC;(不写作法,保留作图痕迹)
-
(2)
当AC=3,BC=4时,△ACP的周长=;
-
18.
(2024·江门模拟)
2022年冬奥会将在中国北京举行,小明和小刚都计划去观看冬奥项目比赛.他们都喜欢的冬奥项目分别是:A.“短道速滑”、B.“冰球”、C.“花样滑冰”和D.“跳台滑雪”.小明和小刚计划各自在这4个冬奥项目中任意选择一个观看,每个项目被选择的可能性相同.
-
(1)
小明选择项目C.“花样滑冰”的概率是多少?
-
(2)
用画树状图或列表的方法,求小明和小刚恰好选择同一项目观看的概率.
四、解答题(二)(本大题共3小题,每小题9分,共27分)
-
19.
(2024·江门模拟)
2023年5月30日,神舟十六号载人飞船发射取得圆满成功,3名航天员顺利进驻中国空间站,如图中的照片展示了中国空间站上机械臂的一种工作状态,当两臂

, 两臂夹角

时,求A,B两点间的距离.(结果精确到

, 参考数据

,

,

)

-
20.
(2024九下·兴宁模拟)
某学校打算购买甲乙两种不同类型的笔记本.已知甲种类型的笔记本的单价比乙种类型的要便宜1元,且用110元购买的甲种类型的数量与用120元购买的乙种类型的数量一样.
-
-
(2)
该学校打算购买甲乙两种类型笔记本共100件,且购买的乙的数量不超过甲的3倍,则购买的最低费用是多少.
-
21.
(2024·江门模拟)
如图,以线段

为直径作

, 交射线

于点

,

平分

交

于点

, 过点

作直线

于点

, 交

的延长线于点

. 连接

并延长交

于点

.
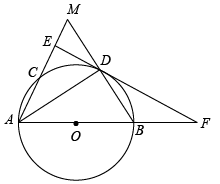
-
(1)
求证:直线

是

的切线;
-
(2)
求证:

;
-
五、解答题(三)(本大题共2小题,每小题12分,共 24分)
-
-
(1)
如图1,在矩形

中,点

,

分别在边

,

上,

, 垂足为点

. 求证:

.
-
-
-
-
-
-
(3)
设线段BD与

轴交于点P,如果点C在

轴上,且

与

相似,求点C的坐标.

 B .
B . 





中,点
,
分别在边
,
上,
, 延长
到点
, 使
, 连接
. 求证:
.
中,点
,
分别在边
,
上,
,
,
, 求
的长.